
 ijУ�߶��꼶��600��ѧ���μ�һ�ο���֪ʶ������Ȼ�������ȡ50��ѧ���ijɼ�����ͳ�Ʒ�����
ijУ�߶��꼶��600��ѧ���μ�һ�ο���֪ʶ������Ȼ�������ȡ50��ѧ���ijɼ�����ͳ�Ʒ�����| ���� | Ƶ�� | Ƶ�� |
| [50��60�� | 5 | 0.1 |
| [60��70�� | 10 | 0.2 |
| [70��80�� | 15 | 0.3 |
| [80��90�� | 15 | 0.3 |
| [90��100�� | 5 | 0.1 |
| �ϼ� | 50 | 1 |
���� ��1������Ƶ��=$\frac{Ƶ��}{��������}$���������Ӧ��Ƶ����$\frac{Ƶ��}{���}$���ɣ�
��2�������������ݻ���Ƶ�ʷֲ�ֱ��ͼ���ɣ�
��3�����ݳɼ���80�����ϵ�Ƶ�ʣ������Ӧ��Ƶ�����ɣ�����Ӧ��Ƶ�����ɣ�
��4������Ƶ�ʷֲ�ֱ��ͼ�и����ο����е������Ӧ�ľ���������ĺͼ�Ϊƽ��ֵ��������������λ���Ķ���������ɣ�
��� �⣺��1������Ƶ��=$\frac{Ƶ��}{��������}$���������Ƶ�ʷֲ�����
| ���� | Ƶ�� | Ƶ�� |
| [50��60�� | 5 | 0.1 |
| [60��70�� | 10 | 0.2 |
| [70��80�� | 15 | 0.3 |
| [80��90�� | 15 | 0.3 |
| [90��100�� | 5 | 0.1 |
| �ϼ� | 50 | 1 |
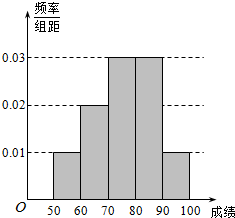
���� ���⿼������Ƶ�ʱ�����Ƶ�ʷֲ�ֱ��ͼ��Ӧ�����⣬�ǻ�����Ŀ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0�� | B�� | 1�� | C�� | 2�� | D�� | ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | -1 | C�� | 0 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 24 | B�� | 22 | C�� | 18 | D�� | 12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| �� | 0 | 1 | 2 |
| p | a | $\frac{1}{3}$ | $\frac{1}{6}$ |
| A�� | $\frac{1}{3}$ | B�� | $\frac{1}{6}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{5}{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | -3 | C�� | $-\frac{{3\sqrt{3}}}{2}$ | D�� | $\frac{{3\sqrt{3}}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com