
分析 (1)由条件令x1=x2,则f(1)=0;(2)由单调性定义,设0<x2<x1,则$\frac{{x}_{1}}{{x}_{2}}$>1,由x>1时,f(x)<0,即有f($\frac{{x}_{1}}{{x}_{2}}$)<0,即可求得单调性(3)关键函数的单调性结合f(x2)>f(9),得到关于x的不等式,解出即可.
解答 解:(1)令x1=x2>0,代入得f(1)=f(x1)-f(x1)=0,故f(1)=0.
(2)任取x1,x2∈(0,+∞),且x1>x2,则$\frac{x_1}{x_2}>1$,由于当x>1时,f(x)<0,
所以$f(\frac{x_1}{x_2})<0$,即f(x1)-f(x2)<0,因此f(x1)<f(x2).
所以函数f(x)在区间(0,+∞)上是单调递减函数.
(3)由$f(\frac{x_1}{x_2})=f({x_1})-f({x_2})$得$f(\frac{9}{3})=f(9)-f(3)$,而f(3)=-1,所以f(9)=-2.
由函数f(x)在区间(0,+∞)上是单调递减函数,且f(x2)>f(9),
得0<x2<9,∴-3<x<0或0<x<3,因此不等式的解集为(-3,0)∪(0,3).
点评 本题考查抽象函数及应用,考查函数的单调性及其应用,注意运用定义,同时考查解决抽象函数的常用方法:赋值法,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
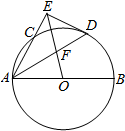 如图,AB是圆O的直径,AC是弦,∠BAC的平分线AD交圆O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.
如图,AB是圆O的直径,AC是弦,∠BAC的平分线AD交圆O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | S={0,1,4,9},T={-3,-2,-1,0,1,2,3},对应法则是开平方 | |
| B. | S={0,1,2,5},T=$\{1,\frac{1}{2},\frac{1}{5}\}$,对应法则是取倒数 | |
| C. | S=N,T={-1,1},对应法则是n→(-1)n,n∈S | |
| D. | S={x|x∈R},T={y|y∈R},对应法则是x→y=$\frac{1+x}{1-x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4,6) | B. | (-4,-6) | C. | (2,2) | D. | (-2,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
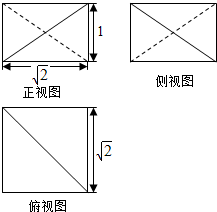
| A. | $\frac{5}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com