
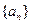 满足:
满足: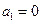 ,
,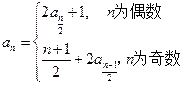
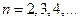
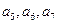 得值;
得值;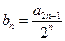 ,试求数列
,试求数列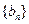 的通项公式;
的通项公式;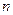 ,试讨论
,试讨论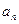 与
与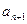 的大小关系。
的大小关系。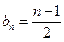 (III)
(III)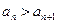
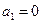 ,
,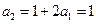 ,
,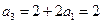 ,
,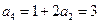 ,
,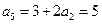 ;
;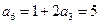 ;
;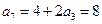 . ………………3分
. ………………3分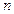 ,都有:
,都有: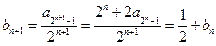 ,
,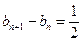 .∴数列
.∴数列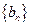 是以
是以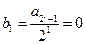 为首项,
为首项,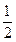 为公差的
为公差的 等差数列.
等差数列.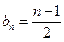 . …………………………………………………
. ………………………………………………… ………7分
………7分 ,
,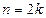 或
或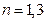 时,
时,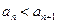 ;
;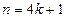 时,
时,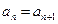 ;
;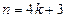 时,
时,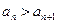 . ……………………………………8分
. ……………………………………8分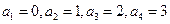 可知
可知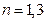 时,
时,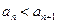 ;
; ,
,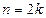 时,
时,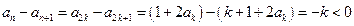 ;
;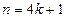 时,
时,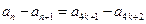
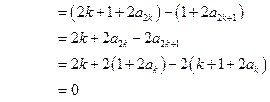
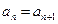 . …………………10分
. …………………10分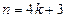 时,
时,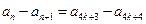
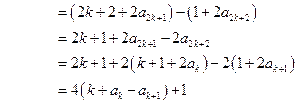
 ,
,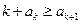 (*)(证明见后),所以,此时,
(*)(证明见后),所以,此时,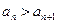 .
. ,
,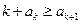 (*)的证明如下:
(*)的证明如下: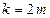 (
(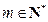 )时,
)时,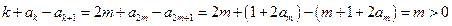 ,
,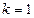 时,
时,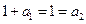 ,满足(*)式。
,满足(*)式。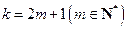 时,
时,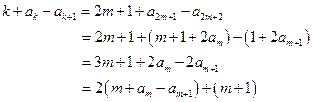
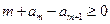 ,如此递推,可归结为1)或2)的情形,于是(*)得证.
,如此递推,可归结为1)或2)的情形,于是(*)得证.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com