
【题目】如图,长途车站P与地铁站O的距离为![]() 千米,从地铁站O出发有两条道路l1,l2,经测量,l1,l2的夹角为45°,OP与l1的夹角
千米,从地铁站O出发有两条道路l1,l2,经测量,l1,l2的夹角为45°,OP与l1的夹角![]() 满足tan
满足tan![]() =
=![]() (其中0<θ<
(其中0<θ<![]() ),现要经过P修条直路分别与道路l1,l2交汇于A,B两点,并在A,B处设立公共自行车停放点.
),现要经过P修条直路分别与道路l1,l2交汇于A,B两点,并在A,B处设立公共自行车停放点.

(1)已知修建道路PA,PB的单位造价分别为2m元/千米和m元/千米,若两段道路的总造价相等,求此时点A,B之间的距离;
(2)考虑环境因素,需要对OA,OB段道路进行翻修,OA,OB段的翻修单价分别为n元/千米和![]() n元/千米,要使两段道路的翻修总价最少,试确定A,B点的位置.
n元/千米,要使两段道路的翻修总价最少,试确定A,B点的位置.
【答案】(1)![]() (2)要使OA,OB段道路的翻修总价最少,A位于距O点3千米处,B位于距点
(2)要使OA,OB段道路的翻修总价最少,A位于距O点3千米处,B位于距点![]() 千米处.
千米处.
【解析】
(1)以O为原点,直线OA为x轴建立平面直角坐标系,得到![]() 的方程,进而求得点P的坐标,
的方程,进而求得点P的坐标,
法一:由题意得![]() ,求得B点的纵坐标为3,进而得到点
,求得B点的纵坐标为3,进而得到点![]() 的坐标,即可得到答案。
的坐标,即可得到答案。
法二:由题意得2mPA=mPB,求得![]() ,根据向量相等,求得点
,根据向量相等,求得点![]() 的坐标,即可求解。
的坐标,即可求解。
(2)法一:由题意,得到造价的表达式![]() ,设
,设![]() ,得到要使S最小,只要y最小,分类讨论,即可求解。
,得到要使S最小,只要y最小,分类讨论,即可求解。
法二:作![]() 交OB于M,交y轴于点Q,作
交OB于M,交y轴于点Q,作![]() 交OA于N,求得OQ=1,进而得到总造价
交OA于N,求得OQ=1,进而得到总造价![]() ,设
,设![]() ,要使S最小,只要y最小,即可求解。
,要使S最小,只要y最小,即可求解。
以O为原点,直线OA为x轴建立平面直角坐标系,
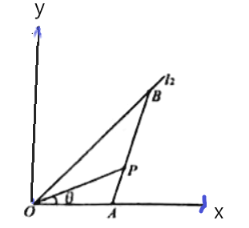
因为![]() ,所以
,所以![]() ,
,
设P(2t,t),由OP=![]() ,得t=1,所以P(2,1)
,得t=1,所以P(2,1)
法一:由题意得![]() ,所以BP=2PA,所以B点的纵坐标为3,
,所以BP=2PA,所以B点的纵坐标为3,
有因为点B在直线![]() 上,所以B(3,3)
上,所以B(3,3)
所以![]() .
.
法二:由题意得2mPA=mPB,所以![]() .
.
设A(a,0)(a>0),又点B在射线y=x(x>0)上,所以可设B(b,b)(b>0),
由![]() ,得
,得![]() 所以
所以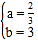
所以![]() .
.
答:A,B之间的距离为![]() 千米.
千米.
(2)法一:设总造价为S.则![]()
设![]() ,要使S最小,只要y最小
,要使S最小,只要y最小
当![]() 轴时,A(2,0),这时OA=2,
轴时,A(2,0),这时OA=2,![]() ,
,
所以![]() .
.
当AB与x轴不垂直时,设直线AB方程为![]() ,
,
令y=0,得点A的横坐标为![]() ,所以
,所以![]() ,
,
令x=y,得点B的横坐标为![]() ,
,
因为![]() 且
且![]() ,所以k<0或k>1,
,所以k<0或k>1,
此时![]() ,
,
![]() ,
,
当k<0时,y在![]() 上递减,在(-1,0)上递增,
上递减,在(-1,0)上递增,
所以![]() ,此时
,此时![]() ;
;
当k>1时,![]()
综上所述,要使OA,OB段道路的翻修总价最少,A位于距O点3千米处,B位于距点![]() 千米处.
千米处.
法二:如图,作![]() 交OB于M,交y轴于点Q
交OB于M,交y轴于点Q
作![]() 交OA于N,困为P(2,1),所以OQ=1
交OA于N,困为P(2,1),所以OQ=1
又因为∠BOQ=45°,所以![]() ,
,
所以![]() ,
,
由![]() ,得
,得![]() ,
,
所以![]() ,
,
设总造价为S,则![]() ,
,
设![]() ,要使S最小,只要y最小.
,要使S最小,只要y最小.
![]()
当且仅当![]() 时取等号,此时
时取等号,此时![]() .
.
答:要使OA,OB段道路的翻修总价最少,位于距O点3千米处,B位于距O点![]() 千米处.
千米处.


科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,侧面B1BCC1是正方形,M,N分别是A1B1,AC的中点,AB⊥平面BCM.
(Ⅰ)求证:平面B1BCC1⊥平面A1ABB1;
(Ⅱ)求证:A1N∥平面BCM;
(Ⅲ)若三棱柱ABC-A1B1C1的体积为10,求棱锥C1-BB1M的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年,国家逐步推行全新的高考制度.新高考不再分文理科.山东省采用3+3模式,其中语文、数学、外语三科为必考科目,每门科目满分均为150分.另外考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物6门科目中自选3门参加考试(6选3),每门科目满分均为100分.为了应对新高考,某高中从高一年级1100名学生(其中男生600人,女生500人)中,采用分层抽样的方法从中抽取n名学生进行调查,其中女生抽取50人.
(1)求n的值;
(2)学校计划在高一上学期开设选修中的“物理”和“地理”两个科目,为了了解学生对这两个科目的选课情况,对抽取到的n名学生进行问卷调查(假定每名学生在“物理”和“地理”这两个科目中必须选择一个科目且只能选择一个科目).下表是根据调查结果得到的一个不完整的2×2列联表,请将下面的2×2列联表补充完整,并判断是否有99%的把握认为选择科目与性别有关?说明你的理由;
选择“物理” | 选择“地理” | 总计 | |
男生 | 10 | ||
女生 | 30 | ||
合计 |
(3)按(2)中选“物理”的男生女生的比例进行分层抽样,从选“物理”的学生中抽出8名学生,再从这8名学生中抽取3人组成物理兴趣小组,设这3人中女生的人数为X,求X的概率分布列及数学期望.
附![]()
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春节前后,一场突如其来的新冠肺炎疫情在全国蔓延.疫情就是命令,防控就是责任.在党中央的坚强领导和统一指挥下,全国人民众志成城、团结一心,掀起了一场坚决打赢疫情防控阻击战的人民战争.下图表展示了2月14日至29日全国新冠肺炎疫情变化情况,根据该折线图,下列结论正确的是( )
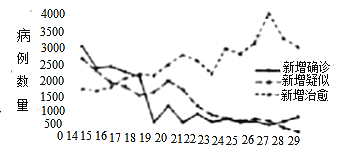
A.16天中每日新增确诊病例数量呈下降趋势且19日的降幅最大
B.16天中每日新增确诊病例的中位数小于新增疑似病例的中位数
C.16天中新增确诊、新增疑似、新增治愈病例的极差均大于2000
D.19日至29日每日新增治愈病例数量均大于新增确诊与新增疑似病例之和
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对![]() 四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”; 乙说:“
作品获得一等奖”; 乙说:“ ![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“ ![]() 两件作品未获得一等奖”; 丁说:“是
两件作品未获得一等奖”; 丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
评奖揭晓后,发现这四位同学中只有两位说的话是对的,则获得一等奖的作品是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年为我国改革开放40周年,某事业单位共有职工600人,其年龄与人数分布表如下:
年龄段 |
|
|
|
|
人数(单位:人) | 180 | 180 | 160 | 80 |
约定:此单位45岁~59岁为中年人,其余为青年人,现按照分层抽样抽取30人作为全市庆祝晚会的观众.
(1)抽出的青年观众与中年观众分别为多少人?
(2)若所抽取出的青年观众与中年观众中分别有12人和5人不热衷关心民生大事,其余人热衷关心民生大事.完成下列![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为年龄层与热衷关心民生大事有关?
的把握认为年龄层与热衷关心民生大事有关?
热衷关心民生大事 | 不热衷关心民生大事 | 总计 | |
青年 | 12 | ||
中年 | 5 | ||
总计 | 30 |
(3)若从热衷关心民生大事的青年观众(其中1人擅长歌舞,3人擅长乐器)中,随机抽取2人上表演节目,则抽出的2人能胜任才艺表演的概率是多少?
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com