
【题目】2020年春节前后,一场突如其来的新冠肺炎疫情在全国蔓延.疫情就是命令,防控就是责任.在党中央的坚强领导和统一指挥下,全国人民众志成城、团结一心,掀起了一场坚决打赢疫情防控阻击战的人民战争.下图表展示了2月14日至29日全国新冠肺炎疫情变化情况,根据该折线图,下列结论正确的是( )
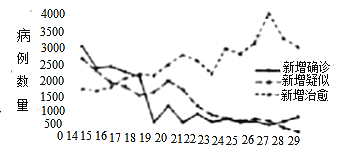
A.16天中每日新增确诊病例数量呈下降趋势且19日的降幅最大
B.16天中每日新增确诊病例的中位数小于新增疑似病例的中位数
C.16天中新增确诊、新增疑似、新增治愈病例的极差均大于2000
D.19日至29日每日新增治愈病例数量均大于新增确诊与新增疑似病例之和
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图像相邻两条对称轴间的距离为
的图像相邻两条对称轴间的距离为![]() ,且
,且![]() ,则以下命题中为假命题的是( )
,则以下命题中为假命题的是( )
A.函数![]() 在
在![]() 上是增函数.
上是增函数.
B.函数![]() 图像关于点
图像关于点![]() 对称
对称
C.函数![]() 的图象可由
的图象可由![]() 的图象向左平移
的图象向左平移![]() 个单位长度得到
个单位长度得到
D.函数![]() 的图象关于直线
的图象关于直线![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
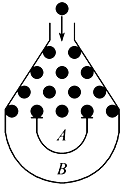
【题目】某超市春节大酬宾,购物满100元可参加一次抽奖活动,规则如下:顾客将一个半径适当的小球放入如图所示的容器正上方的人口处,小球在自由落下的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中,顾客相应获得袋子里的奖品.已知小球每次遇到黑色障碍物时,向左向右下落的概率都为![]() .若活动当天小明在该超市购物消费108元,按照活动规则,他可参加一次抽奖,则小明获得A袋中的奖品的概率为_____.
.若活动当天小明在该超市购物消费108元,按照活动规则,他可参加一次抽奖,则小明获得A袋中的奖品的概率为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长途车站P与地铁站O的距离为![]() 千米,从地铁站O出发有两条道路l1,l2,经测量,l1,l2的夹角为45°,OP与l1的夹角
千米,从地铁站O出发有两条道路l1,l2,经测量,l1,l2的夹角为45°,OP与l1的夹角![]() 满足tan
满足tan![]() =
=![]() (其中0<θ<
(其中0<θ<![]() ),现要经过P修条直路分别与道路l1,l2交汇于A,B两点,并在A,B处设立公共自行车停放点.
),现要经过P修条直路分别与道路l1,l2交汇于A,B两点,并在A,B处设立公共自行车停放点.

(1)已知修建道路PA,PB的单位造价分别为2m元/千米和m元/千米,若两段道路的总造价相等,求此时点A,B之间的距离;
(2)考虑环境因素,需要对OA,OB段道路进行翻修,OA,OB段的翻修单价分别为n元/千米和![]() n元/千米,要使两段道路的翻修总价最少,试确定A,B点的位置.
n元/千米,要使两段道路的翻修总价最少,试确定A,B点的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (a,b
(a,b![]() R).
R).
(1)当a=b=1时,求![]() 的单调增区间;
的单调增区间;
(2)当a≠0时,若函数![]() 恰有两个不同的零点,求
恰有两个不同的零点,求![]() 的值;
的值;
(3)当a=0时,若![]() 的解集为(m,n),且(m,n)中有且仅有一个整数,求实数b的取值范围.
的解集为(m,n),且(m,n)中有且仅有一个整数,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长途车站P与地铁站O的距离为![]() 千米,从地铁站O出发有两条道路l1,l2,经测量,l1,l2的夹角为45°,OP与l1的夹角
千米,从地铁站O出发有两条道路l1,l2,经测量,l1,l2的夹角为45°,OP与l1的夹角![]() 满足tan
满足tan![]() =
=![]() (其中0<θ<
(其中0<θ<![]() ),现要经过P修条直路分别与道路l1,l2交汇于A,B两点,并在A,B处设立公共自行车停放点.
),现要经过P修条直路分别与道路l1,l2交汇于A,B两点,并在A,B处设立公共自行车停放点.

(1)已知修建道路PA,PB的单位造价分别为2m元/千米和m元/千米,若两段道路的总造价相等,求此时点A,B之间的距离;
(2)考虑环境因素,需要对OA,OB段道路进行翻修,OA,OB段的翻修单价分别为n元/千米和![]() n元/千米,要使两段道路的翻修总价最少,试确定A,B点的位置.
n元/千米,要使两段道路的翻修总价最少,试确定A,B点的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点F(1,0),O为坐标原点,A,B是抛物线C上异于 O的两点.
的焦点F(1,0),O为坐标原点,A,B是抛物线C上异于 O的两点.
(1)求抛物线C的方程;
(2)若直线AB过点(8,0),求证:直线OA,OB的斜率之积为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(3-x)ex,g(x)=x+a(a∈R)(e是自然对数的底数,e≈2.718…).
(1)求函数f(x)的极值;
(2)若函数y=f(x)g(x)在区间[1,2]上单调递增,求实数a的取值范围;
(3)若函数h(x)=![]() 在区间(0,+∞)上既存在极大值又存在极小值,并且函数h(x)的极大值小于整数b,求b的最小值.
在区间(0,+∞)上既存在极大值又存在极小值,并且函数h(x)的极大值小于整数b,求b的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com