
【题目】已知函数![]() (a,b
(a,b![]() R).
R).
(1)当a=b=1时,求![]() 的单调增区间;
的单调增区间;
(2)当a≠0时,若函数![]() 恰有两个不同的零点,求
恰有两个不同的零点,求![]() 的值;
的值;
(3)当a=0时,若![]() 的解集为(m,n),且(m,n)中有且仅有一个整数,求实数b的取值范围.
的解集为(m,n),且(m,n)中有且仅有一个整数,求实数b的取值范围.
【答案】(1)f(x)的单调增区间是![]() 和
和![]()
(2)![]()
(3)![]()
【解析】
(1)当a=b=1时,求得函数的导数,即可求解函数的单调区间;
(2)法一:求得![]() ,令
,令![]() ,得
,得![]() 或
或![]() ,由函数f(x)有两个不同的零点,求得
,由函数f(x)有两个不同的零点,求得![]() 的方程,即可求解;
的方程,即可求解;
法二:由![]() 得,
得,![]() ,设
,设![]() ,利用导数求得函数的单调区间和极值,进而可得函数的零点。
,利用导数求得函数的单调区间和极值,进而可得函数的零点。
(3)当![]() 时,可得
时,可得![]() ,设
,设![]() ,利用导数得到函数的单调区间和极值,转化为要使
,利用导数得到函数的单调区间和极值,转化为要使![]() 有解,和
有解,和![]() 的解集(m,n)中只有一个整数,分别列出不等式组,即可求解。
的解集(m,n)中只有一个整数,分别列出不等式组,即可求解。
(1)当a=b=1时,![]() ,
,
令![]() ,解得
,解得![]() 或
或![]()
所以f(x)的单调增区间是![]() 和
和![]()
(2)法一:![]() ,令
,令![]() ,得
,得![]() 或
或![]() ,
,
因为函数f(x)有两个不同的零点,所以![]() 或
或![]() ,
,
当![]() 时,得a=0,不合题意,舍去:
时,得a=0,不合题意,舍去:
当![]() 时,代入得
时,代入得![]()
即![]() ,所以
,所以![]() .
.
法二:由于![]() ,所以
,所以![]() ,
,
由![]() 得,
得,![]() ,
,
设![]() ,
,![]() 令
令![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,h(x)递减:当
,h(x)递减:当![]() 时,
时,![]() ,
,![]() 递增
递增
当![]() 时,
时,![]() ,
,![]() 单调递增
单调递增
当![]() 时,
时, ![]() 的值域为R
的值域为R
故不论![]() 取何值,方程
取何值,方程![]() 有且仅有一个根;
有且仅有一个根;
当![]() 时,
时,![]() ,
,
所以![]() 时,方程
时,方程![]() 恰有一个根-2,
恰有一个根-2,
此时函数![]() 恰有两个零点-2和1.
恰有两个零点-2和1.
(3)当![]() 时,因为
时,因为![]() ,所以
,所以![]()
设![]() ,则
,则![]() ,
,
当![]() 时,因为
时,因为![]() ,所以
,所以![]() 在
在![]() 上递增,且
上递增,且![]() ,
,
所以在![]() 上,
上,![]() ,不合题意:
,不合题意:
当![]() 时,令
时,令![]() ,得
,得![]() ,
,
所以![]() 在
在![]() 递增,在
递增,在![]() 递减,
递减,
所以![]() ,
,
要使![]() 有解,首先要满足
有解,首先要满足![]() ,解得
,解得![]() . ①
. ①
又因为![]() ,
,![]() ,
,
要使![]() 的解集(m,n)中只有一个整数,则
的解集(m,n)中只有一个整数,则![]()
即![]() 解得
解得![]() . ②
. ②
设![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 递增:当
递增:当![]() 时,
时,![]() ,
,![]() 递减
递减
所以![]() ,所以
,所以![]() ,
,
所以由①和②得,![]() .
.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数 f(x) = ![]() -ax(a > 0).
-ax(a > 0).
(1) 当 a = 1 时,求证:对于任意 x > 0,都有 f(x) > 0 成立;
(2) 若函数 y = f(x) 恰好在 x = x1 和 x = x2 两处取得极值,求证:![]() < ln a.
< ln a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国于2015年10月宣布实施普遍二孩政策,为了解户籍、性别对生育二胎选择倾向的影响,某地从育龄群体中随机抽取了容量为140的调查样本,其中城镇户籍与农村户籍各70人;男性60人,女性80人,绘制的不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例如图所示,其中阴影部分表示倾向选择生育二胎的对应比例,则下列叙述正确的是( )
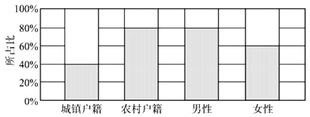
A.是否倾向选择生育二胎与户籍有关
B.是否倾向选择生育二胎与性别有关
C.调查样本里面倾向选择生育二胎的人群中,男性人数少于女性人数
D.倾向选择不生育二胎的人群中,农村户籍人数多于城镇户籍人数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某种螺帽是由一个半径为2的半球体挖去一个正三棱锥构成的几何体,该正三棱锥的底面三角形内接于半球底面大圆,顶点在半球面上,则被挖去的正三棱锥体积为_______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位同学参加诗词大赛,各答3道题,每人答对每道题的概率均为![]() ,且各人是否答对每道题互不影响.
,且各人是否答对每道题互不影响.
(Ⅰ)用![]() 表示甲同学答对题目的个数,求随机变量
表示甲同学答对题目的个数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)设![]() 为事件“甲比乙答对题目数恰好多2”,求事件
为事件“甲比乙答对题目数恰好多2”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春节前后,一场突如其来的新冠肺炎疫情在全国蔓延.疫情就是命令,防控就是责任.在党中央的坚强领导和统一指挥下,全国人民众志成城、团结一心,掀起了一场坚决打赢疫情防控阻击战的人民战争.下图表展示了2月14日至29日全国新冠肺炎疫情变化情况,根据该折线图,下列结论正确的是( )
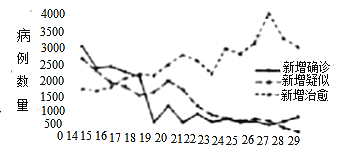
A.16天中每日新增确诊病例数量呈下降趋势且19日的降幅最大
B.16天中每日新增确诊病例的中位数小于新增疑似病例的中位数
C.16天中新增确诊、新增疑似、新增治愈病例的极差均大于2000
D.19日至29日每日新增治愈病例数量均大于新增确诊与新增疑似病例之和
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为评估设备![]() 生产某种零件的性能,从设备
生产某种零件的性能,从设备![]() 生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
直径 | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合计 |
件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
经计算,样本的平均值![]() ,标准差
,标准差![]() ,以频率值作为概率的估计值.
,以频率值作为概率的估计值.
(1)由以往统计数据知,设备的性能根据以下不等式进行评判(![]() 表示相应事件的概率);①
表示相应事件的概率);①![]() ;②
;②![]() ;③
;③![]() ,评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁.为评判一台设备
,评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁.为评判一台设备![]() 的性能,从该设备加工的零件中任意抽取一件,记其直径为
的性能,从该设备加工的零件中任意抽取一件,记其直径为![]() ,试判断设备
,试判断设备![]() 的性能等级
的性能等级
(2)将直径小于等于![]() 或直径大于
或直径大于![]() 的零件认为是次品.
的零件认为是次品.
(i)若从设备![]() 的生产流水线上随意抽取2件零件,求恰有一件次品的概率;
的生产流水线上随意抽取2件零件,求恰有一件次品的概率;
(ii)若从样本中随意抽取2件零件,计算其中次品个数![]() 分布列和数学期望
分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙两名工人在同样条件下每天各生产100件产品,且每生产1件正品可获利20元,生产1件次品损失30元,甲,乙两名工人100天中出现次品件数的情况如表所示.
甲每天生产的次品数/件 | 0 | 1 | 2 | 3 | 4 |
对应的天数/天 | 40 | 20 | 20 | 10 | 10 |
乙每天生产的次品数/件 | 0 | 1 | 2 | 3 |
对应的天数/天 | 30 | 25 | 25 | 20 |
(1)将甲每天生产的次品数记为![]() (单位:件),日利润记为
(单位:件),日利润记为![]() (单位:元),写出
(单位:元),写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)如果将统计的100天中产生次品量的频率作为概率,记![]() 表示甲、乙两名工人1天中各自日利润不少于1950元的人数之和,求随机变量
表示甲、乙两名工人1天中各自日利润不少于1950元的人数之和,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com