
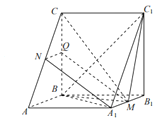
【题目】如图,在三棱柱ABC-A1B1C1中,侧面B1BCC1是正方形,M,N分别是A1B1,AC的中点,AB⊥平面BCM.
(Ⅰ)求证:平面B1BCC1⊥平面A1ABB1;
(Ⅱ)求证:A1N∥平面BCM;
(Ⅲ)若三棱柱ABC-A1B1C1的体积为10,求棱锥C1-BB1M的体积.

【答案】(Ⅰ)详见解析(Ⅱ)详见解析(Ⅲ)![]()
【解析】
(Ⅰ)推导出AB⊥BC,BB1⊥BC,从而BC⊥平面A1ABB1,由此能证明平面B1BCC1⊥平面A1ABB1.
(Ⅱ)设BC中点为Q,连结NQ,MQ,推导出四边形A1MQN是平行四边形,从而A1N∥MQ,由此能证明A1N∥平面BCM.
(Ⅲ)连结A1B,根据棱柱和棱锥的体积公式,三棱锥B﹣A1B1C1的体积![]() ,棱锥C1﹣BB1M的体积
,棱锥C1﹣BB1M的体积![]() ,由此能求出结果.
,由此能求出结果.
证明:(Ⅰ)∵AB⊥平面BCM,BC平面BCM,∴AB⊥BC,
∵正方形B1BCC1,∴BB1⊥BC,
∵AB∩BB1=B,∴BC⊥平面A1ABB1,
∵BC平面B1BCC1,∴平面B1BCC1⊥平面A1ABB1;
(Ⅱ)设BC中点为Q,连结NQ,MQ,
∵M,N分别是A1B1,AC的中点,∴NQ∥AB,且NQ=![]() AB,
AB,
∵AB∥A1B1,且AB=A1B1,∴NQ∥A1M,且NQ=A1M,
∴四边形A1MQN是平行四边形,∴A1N∥MQ,
∵MQ平面BCM,A1N
∴A1N∥平面BCM.
(Ⅲ)连结A1B,根据棱柱和棱锥的体积公式,
得到三棱锥B-A1B1C1的体积![]() =
=![]() =
=![]() ,
,
∵M为A1B1的中点,
∴棱锥C1-BB1M的体积![]() =
=![]() =
=![]() =
=![]() .
.


科目:高中数学 来源: 题型:
【题目】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校所有的1000名学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付方式 | 不大于2000元 | 大于2000元 |
仅使用A | 27人 | 3人 |
仅使用B | 24人 | 1人 |
(Ⅰ)估计该校学生中上个月A,B两种支付方式都使用的人数;
(Ⅱ)从样本仅使用B的学生中随机抽取1人,求该学生上个月支付金额大于2000元的概率;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用B的学生中随机抽查1人,发现他本月的支付金额大于2000元.结合(Ⅱ)的结果,能否认为样本仅使用B的学生中本月支付金额大于2000元的人数有变化?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大提出对农村要坚持精准扶贫,至 2020 年底全面脱贫. 现有扶贫工作组到某山区贫困村实施脱贫工作. 经摸底排查,该村现有贫困农户 100 家,他们均从事水果种植, 2017 年底该村平均每户年纯收入为 1 万元,扶贫工作组一方面请有关专家对水果进行品种改良,提高产量;另一方面,抽出部分农户从事水果包装、销售工作,其人数必须小于种植的人数. 从 2018 年初开始,若该村抽出 5x 户( x ∈Z,1 ≤x ≤ 9) 从事水果包装、销售.经测算,剩下从事水果种植农户的年纯收入每户平均比上一年提高![]() ,而从事包装销售农户的年纯收入每户平均为 (3-
,而从事包装销售农户的年纯收入每户平均为 (3-![]() x) 万元(参考数据: 1.13 = 1.331,1.153 ≈ 1.521,1.23 = 1.728).
x) 万元(参考数据: 1.13 = 1.331,1.153 ≈ 1.521,1.23 = 1.728).
(1) 至 2020 年底,为使从事水果种植农户能实现脱贫(每户年均纯收入不低于 1 万 6 千元),至少抽出多少户从事包装、销售工作?
(2) 至 2018 年底,该村每户年均纯收人能否达到 1.35 万元?若能,请求出从事包装、销售的户数;若不能,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图像相邻两条对称轴间的距离为
的图像相邻两条对称轴间的距离为![]() ,且
,且![]() ,则以下命题中为假命题的是( )
,则以下命题中为假命题的是( )
A.函数![]() 在
在![]() 上是增函数.
上是增函数.
B.函数![]() 图像关于点
图像关于点![]() 对称
对称
C.函数![]() 的图象可由
的图象可由![]() 的图象向左平移
的图象向左平移![]() 个单位长度得到
个单位长度得到
D.函数![]() 的图象关于直线
的图象关于直线![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校课题组为了研究学生的数学成绩与学生细心程度的关系,在本校随机调查了100名学生进行研究.研究结果表明:在数学成绩及格的50名学生中有40人比较细心,另外10人比较粗心;在数学成绩不及格的50名学生中有20人比较细心,另外30人比较粗心.
(1)试根据上述数据完成![]() 列联表:
列联表:
数学成绩及格 | 数学成绩不及格 | 合计 | |
比较细心 | 40 | ||
比较粗心 | |||
合计 | 50 | 100 |
(2)能否在犯错误的概率不超过0.001的前提下认为学生的数学成绩与细心程度有关系?
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某公园内有两条道路![]() ,
,![]() ,现计划在
,现计划在![]() 上选择一点
上选择一点![]() ,新建道路
,新建道路![]() ,并把
,并把![]() 所在的区域改造成绿化区域.已知
所在的区域改造成绿化区域.已知![]() ,
,![]()
![]() .
.
(1)若绿化区域![]() 的面积为1
的面积为1![]() ,求道路
,求道路![]() 的长度;
的长度;
(2)若绿化区域![]() 改造成本为10万元/
改造成本为10万元/![]() ,新建道路
,新建道路![]() 成本为10万元/
成本为10万元/![]() .设
.设![]() (
(![]() ),当
),当![]() 为何值时,该计划所需总费用最小?
为何值时,该计划所需总费用最小?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点与椭圆
的焦点与椭圆![]() 的一个焦点重合,椭圆
的一个焦点重合,椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,
,![]() 是椭圆
是椭圆![]() 上一点,记直线
上一点,记直线![]() 的斜率为
的斜率为![]() 、
、![]() ,且有
,且有![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 与椭圆相交于不同两点
与椭圆相交于不同两点![]() 和
和![]() ,且满足
,且满足![]() (
(![]() 为坐标原点),求实数
为坐标原点),求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长途车站P与地铁站O的距离为![]() 千米,从地铁站O出发有两条道路l1,l2,经测量,l1,l2的夹角为45°,OP与l1的夹角
千米,从地铁站O出发有两条道路l1,l2,经测量,l1,l2的夹角为45°,OP与l1的夹角![]() 满足tan
满足tan![]() =
=![]() (其中0<θ<
(其中0<θ<![]() ),现要经过P修条直路分别与道路l1,l2交汇于A,B两点,并在A,B处设立公共自行车停放点.
),现要经过P修条直路分别与道路l1,l2交汇于A,B两点,并在A,B处设立公共自行车停放点.

(1)已知修建道路PA,PB的单位造价分别为2m元/千米和m元/千米,若两段道路的总造价相等,求此时点A,B之间的距离;
(2)考虑环境因素,需要对OA,OB段道路进行翻修,OA,OB段的翻修单价分别为n元/千米和![]() n元/千米,要使两段道路的翻修总价最少,试确定A,B点的位置.
n元/千米,要使两段道路的翻修总价最少,试确定A,B点的位置.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com