Question

9．定义区间（c，d）、（c，d]、[c，d）、[c，d]的长度均为d-c（d＞c），己知实数p＞0，则满足不等式$\frac{1}{x-p}$+$\frac{1}{x}$≥1的x构成的区间长度之和为2．

Answer 1

分析 原不等式化为$\frac{{x}^{2}-（p+2）x+p}{x（x-p）}$≤0，设x²-（p+2）x+p=0的根为x₁和x₂，则由求根公式可得这两个根的值，结合数轴，用穿根法来解的不等式的解集，从而求得解集构成的区间的长度之和．

解答 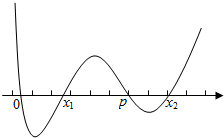解：∵$\frac{1}{x-p}$+$\frac{1}{x}$≥1，实数p＞0，∴$\frac{2x-p}{x（x-p）}$≥1，即$\frac{{x}^{2}-（p+2）x+p}{x（x-p）}$≤0，
设x²-（p+2）x+p=0的根为x₁和x₂，则由求根公式可得，
x₁=$\frac{p+2-\sqrt{{p}^{2}+4}}{2}$，x₂=$\frac{p+2+\sqrt{{p}^{2}+4}}{2}$，
把不等式的根排在数轴上，
由穿根得不等式的解集为（0，x₁）∪（p，x₂ ），故解集构成的区间的长度之和为 （x₁-0）+（x₂-p ）
=（x₁+x₂ ）-p=（p+2）-p=2，
故答案为：2．

点评 本题考查其他不等式的解法，解题的关键是掌握用穿根法解分式不等式和高次不等式的技巧，本题中令分子为0，得出x₁和x₂与系数的关系对解本题尤其关键．本题考查数形结合的思想，是不等式求解中难度较大的题型．