
分析 由题意可知三棱锥P-ABC是长方体的一个角,该长方体的对角线的长就是经过P、A、B、C四点的球的直径,利用长方体对角线长公式算出球的直径,从而得到球的半径,再由球的表面积公式加以计算,可得答案.
解答 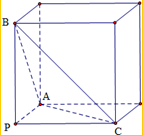 解:根据题意,可知三棱锥P-ABC是长方体的一个角,该长方体的外接球就是经过P,A,B,C四点的球
解:根据题意,可知三棱锥P-ABC是长方体的一个角,该长方体的外接球就是经过P,A,B,C四点的球
∵$PA=3,PB=4,PC=5\sqrt{3}$,
∴长方体的对角线的长为$\sqrt{P{A}^{2}+P{B}^{2}+P{C}^{2}}$=10,
即外接球的直径2R=10,可得R=5,
因此,外接球的表面积为S=4πR2=4π×52=100π
故答案为:100π.
点评 本题给出三条侧棱两两垂直的三棱锥,求它的外接球的表面积.着重考查了长方体对角线公式、球内接多面体和球的表面积公式等知识,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知抛物线y2=2px(p>0)的焦点为F与椭圆C的一个焦点重合,且抛物线的准线与椭圆C相交于点$({-1,\frac{{\sqrt{2}}}{2}})$.
已知抛物线y2=2px(p>0)的焦点为F与椭圆C的一个焦点重合,且抛物线的准线与椭圆C相交于点$({-1,\frac{{\sqrt{2}}}{2}})$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com