
 已知抛物线y2=2px(p>0)的焦点为F与椭圆C的一个焦点重合,且抛物线的准线与椭圆C相交于点$({-1,\frac{{\sqrt{2}}}{2}})$.
已知抛物线y2=2px(p>0)的焦点为F与椭圆C的一个焦点重合,且抛物线的准线与椭圆C相交于点$({-1,\frac{{\sqrt{2}}}{2}})$.分析 (1)由已知求得p,则抛物线方程可求;
(2)设出椭圆方程,由已知列关于a,b,c的方程组,求得a,b的值,得到椭圆方程,当直线l的斜率不存在时,不合题意;当直线l的斜率存在时,设正方形第三个顶点坐标为P(0,y0),设出直线方程y=k(x-1)(k≠0),联立直线方程和椭圆方程,利用根与系数的关系结合$\overrightarrow{PM}•\overrightarrow{PN}=0$求得k值.
解答 解:(1)由题意知,$-\frac{p}{2}=-1$,则p=2,
∴抛物线方程为y2=4x;
(2)设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$,
则$\left\{\begin{array}{l}{c=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\\{\frac{1}{{a}^{2}}+\frac{1}{2{b}^{2}}=1}\end{array}\right.$,解得a2=2,b2=1.
∴椭圆C的方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$.
若l垂直于x轴,得M(1,-$\frac{\sqrt{2}}{2}$),N(1,$\frac{\sqrt{2}}{2}$),$\overrightarrow{OM}•\overrightarrow{ON}=1-\frac{1}{2}=\frac{1}{2}$,不符合;
若l不垂直于x轴,
设正方形第三个顶点坐标为P(0,y0),M(x1,y1),N(x2,y2)
令l:y=k(x-1)(k≠0),代入$\frac{{x}^{2}}{2}+{y}^{2}=1$,得(1+2k2)x2-4k2x+2k2-2=0.
∴${x}_{1}+{x}_{2}=\frac{4{k}^{2}}{1+2{k}^{2}},{x}_{1}{x}_{2}=\frac{2{k}^{2}-2}{1+2{k}^{2}}$,
y1+y2=k(x1+x2)-2k=$k•\frac{4{k}^{2}}{1+2{k}^{2}}-2k=\frac{-2k}{1+2{k}^{2}}$,
则线段MN的中垂线方程为$y+\frac{k}{1+2{k}^{2}}=-\frac{1}{k}(x-\frac{{k}^{2}-1}{1+2{k}^{2}})$,
∴P(0,$-\frac{1}{k(1+2{k}^{2})}$).
由$\overrightarrow{PM}•\overrightarrow{PN}=0$,得x1x2+(y1-y0)(y2-y0)=0.
即${{y}_{0}}^{2}+\frac{2k}{1+2{k}^{2}}{y}_{0}=0$(y0≠0),∴${y}_{0}=-\frac{2k}{1+2{k}^{2}}$,
又${y}_{0}=-\frac{1}{k(1+2{k}^{2})}$,∴$-\frac{2k}{1+2{k}^{2}}=-\frac{1}{k(1+2{k}^{2})}$,解得k=$±\frac{\sqrt{2}}{2}$.
∴直线l的方程为$y=±\frac{\sqrt{2}}{2}(x-1)$.
点评 本题考查椭圆方程与抛物线方程的求法,考查了直线与圆锥曲线的位置关系的应用,训练了平面向量在求解圆锥曲线问题中的应用,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
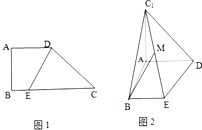 如图1,直角梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=$\frac{1}{2}$BC=1,E是底边BC上的一点,且EC=3BE.现将△CDE沿DE折起到△C1DE的位置,得到如图2所示的四棱锥C1-ABED,且C1A=AB.
如图1,直角梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=$\frac{1}{2}$BC=1,E是底边BC上的一点,且EC=3BE.现将△CDE沿DE折起到△C1DE的位置,得到如图2所示的四棱锥C1-ABED,且C1A=AB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $a<\frac{1}{3}$ | B. | $a≤\frac{1}{3}$ | C. | $a>\frac{1}{3}$ | D. | $a≥\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x2 | B. | y=3x | C. | y=sinx | D. | y=log${\;}_{\frac{1}{2}}$(x+1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com