
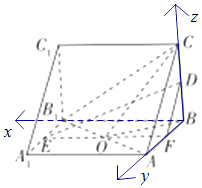
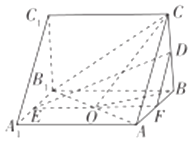
【题目】在如图所示的三棱锥ABC﹣A1B1C1中,AA1⊥底面ABC,D,E分别是BC,A1B1的中点. 
(1)求证:DE∥平面ACC1A1;
(2)若AB⊥BC,AB=BC,∠ACB1=60°,求直线BC与平面AB1C所成角的正切值.
【答案】
(1)解:取AB的中点F,连接DF,EF
在△ABC中,因为D,F分别为BC,AB的中点,
所以DF∥AC(中位线),
又∵DF平面ACC1A1,AC平面ACC1A1,
所以DF∥平面ACC1A1
在矩形ABB1A1中,因为E,F分别为A1B1,AB的中点,
∴EF∥AA1(中位线),
又∵EF平面 ACC1A1,AA1平面ACC1A1,
∴EF∥平面ACC1A1
∵DF∩EF=F,
∴平面DEF∥平面ACC1A1
∵DE平面DEF,
∴DE∥平面ACC1A1
(2)解:解法一:
∵三棱柱ABC﹣A1B1C1为直三棱柱,
∴BC⊥BB1,
又AB⊥BC,AB∩BB1=B,
∴BC⊥平面ABB1A1,
∵AB=BC,BB1=BB1,
∴△ABB1≌△CBB1
∴AB1=CB1,又 ![]() ,
,
∴△AB1C为正三角形,
∴ ![]() ,∴BB1=AB
,∴BB1=AB
取AB1的中点O,连接BO,CO,
∴AB1⊥BO,AB1⊥CO,
∴AB1⊥平面BCO,
∴平面AB1C⊥平面BCO,点B在平面AB1C上的射影在CO上,
∴∠BCO即为直线BC与平面AB1C所成角
在Rt△BCO中, ![]() ,
,
∴ ![]()
解法二:由题知BB1,BA,BC两两互相垂直,故建立空间直角坐标线如图,
并设AB=2,BB1=t,
则A(0,2,0),C(0,0,2),B1(t,0,0)(t>0)
∴ ![]() ,
, ![]()
∵ ![]() ,∴
,∴ ![]() =60°
=60°
∴ ![]() ,得t=2.
,得t=2.
∴B1(2,0,0), ![]() ,
,
设平面AB1C的法向量为 ![]()
则 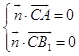 得x=y=z,取
得x=y=z,取 ![]() =(1,1,1)
=(1,1,1)
记直线BC与平面AB1C所成角为θ,且 ![]()
则 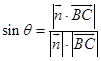 =
= ![]()
∴ ![]()
故直线BC与平面AB1C所成角的正切值为 ![]() .
.
【解析】(1)根据题目特点,可由证面面平行,得到线面平行.(2)方法一:找出线面所成角,再构造三角形求线面角的正切值;方法二:建立空间直角坐标系,根据向量所成角,求得线面角.
【考点精析】掌握直线与平面平行的判定和空间角的异面直线所成的角是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则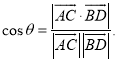 .
.


科目:高中数学 来源: 题型:
【题目】若关于某设备的使用年限x(年)和所支出的维修费y(万元)有如下统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知,y对x呈线性相关关系.
(1) 请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]()
![]() ;
;
(2) 估计使用年限为10年时,试求维修费用约是多少?(精确到两位小数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线y=![]() 焦点F的直线交抛物线于A,B两点,点C在直线y=-1上,若△ABC为正三角形,则其边长为
焦点F的直线交抛物线于A,B两点,点C在直线y=-1上,若△ABC为正三角形,则其边长为
A. 11 B. 13 C. 14 D. 12
查看答案和解析>>
科目:高中数学 来源: 题型:
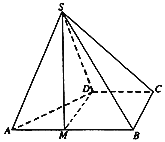
【题目】四棱锥S-ABCD的底面ABCD为直角梯形,AB∥CD,AB⊥BC,AB=2BC=2CD=2,△SAD为正三角形.
(Ⅰ)点M为棱AB上一点,若BC∥平面SDM,AM=λAB,求实数λ的值;
(Ⅱ)若BC⊥SD,求二面角A-SB-C的余弦值.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
(Ⅰ)由线面平行的性质定理可得![]() ,据此可知四边形BCDM为平行四边形,据此可得
,据此可知四边形BCDM为平行四边形,据此可得![]() .
.
(Ⅱ)由几何关系,在平面![]() 内过点
内过点![]() 作
作![]() 直线
直线![]() 于点
于点![]() ,以点E为坐标原点,EA方向为X轴,EC方向为Y轴,ES方向为Z轴建立空间坐标系,据此可得平面
,以点E为坐标原点,EA方向为X轴,EC方向为Y轴,ES方向为Z轴建立空间坐标系,据此可得平面![]() 的一个法向量
的一个法向量![]() ,平面
,平面![]() 的一个法向量
的一个法向量![]() ,据此计算可得二面角
,据此计算可得二面角![]() 余弦值为
余弦值为![]() .
.
(Ⅰ)因为![]() 平面SDM,
平面SDM,![]()
![]() 平面ABCD,平面SDM
平面ABCD,平面SDM ![]() 平面ABCD=DM,所以
平面ABCD=DM,所以![]() ,
,
因为![]() ,所以四边形BCDM为平行四边形,又
,所以四边形BCDM为平行四边形,又![]() ,所以M为AB的中点.
,所以M为AB的中点.
因为![]()
![]() .
.

(Ⅱ)因为![]()
![]() ,
, ![]()
![]() ,所以
,所以![]() 平面
平面![]() ,又因为
,又因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
在平面![]() 内过点
内过点![]() 作
作![]() 直线
直线![]() 于点
于点![]() ,则
,则![]() 平面
平面![]() ,
,
在![]() 和
和![]() 中,因为
中,因为![]() ,所以
,所以![]() ,
,
又由题知![]() ,所以
,所以![]() 所以
所以![]() ,
,
以下建系求解.以点E为坐标原点,EA方向为X轴,EC方向为Y轴,ES方向为Z轴建立如图所示空间坐标系,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,则
,则 ,所
,所![]() ,
,
令![]() 得
得![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
同理得![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
 ,因为二面角
,因为二面角![]() 为钝角.
为钝角.
所以二面角![]() 余弦值为
余弦值为![]() .
.
【点睛】
本题考查了立体几何中的判断定理和二面角的求解问题,意在考查学生的空间想象能力和逻辑推理能力;解答本题关键在于能利用直线与直线、直线与平面、平面与平面关系的相互转化,通过严密推理,明确角的构成.同时对于立体几何中角的计算问题,往往可以利用空间向量法,通过求解平面的法向量,利用向量的夹角公式求解.
【题型】解答题
【结束】
19
【题目】小明在石家庄市某物流派送公司找到了一份派送员的工作,该公司给出了两种日薪薪酬方案.甲方案:底薪100元,每派送一单奖励1元;乙方案:底薪140元,每日前55单没有奖励,超过55单的部分每单奖励12元.
(Ⅰ)请分别求出甲、乙两种薪酬方案中日薪y(单位:元)与送货单数n的函数关系式;
(Ⅱ)根据该公司所有派送员100天的派送记录,发现派送员的日平均派送单数满足以下条件:在这100天中的派送量指标满足如图所示的直方图,其中当某天的派送量指标在(![]() ,
,![]() ](n=1,2,3,4,5)时,日平均派送量为50+2n单.若将频率视为概率,回答下列问题:
](n=1,2,3,4,5)时,日平均派送量为50+2n单.若将频率视为概率,回答下列问题:
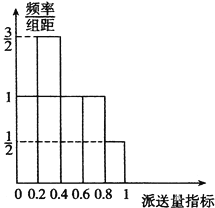
①根据以上数据,设每名派送员的日薪为X(单位:元),试分别求出甲、乙两种方案的日薪X的分布列,数学期望及方差;
②结合①中的数据,根据统计学的思想,帮助小明分析,他选择哪种薪酬方案比较合适,并说明你的理由。
(参考数据:0.62=0.36,1.42=1.9 6,2.6 2=6.76,3.42=1 1.56,3.62=12.96,4.62=21.16,15.62=243.36,20.42=416.16,44.42=1971.36)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某路段最高限速60km/h,电子监控测得连续6辆汽车的速度用茎叶图表示如下(单位:km/h).若从中任取2辆,则恰好有1辆汽车超速的概率为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某房地产开发商为吸引更多消费者购房,决定在一块闲置的扇形空地中修建一个花园.如图,已知扇形AOB的圆心角∠AOB=![]() ,半径为R.现欲修建的花园为OMNH,其中M,H分别在OA,OB上,N在
,半径为R.现欲修建的花园为OMNH,其中M,H分别在OA,OB上,N在![]() 上.设∠MON=θ,OMNH的面积为S.
上.设∠MON=θ,OMNH的面积为S.

(1)将S表示为关于θ的函数;
(2)求S的最大值及相应的θ值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com