
【题目】某房地产开发商为吸引更多消费者购房,决定在一块闲置的扇形空地中修建一个花园.如图,已知扇形AOB的圆心角∠AOB=![]() ,半径为R.现欲修建的花园为OMNH,其中M,H分别在OA,OB上,N在
,半径为R.现欲修建的花园为OMNH,其中M,H分别在OA,OB上,N在![]() 上.设∠MON=θ,OMNH的面积为S.
上.设∠MON=θ,OMNH的面积为S.

(1)将S表示为关于θ的函数;
(2)求S的最大值及相应的θ值.
【答案】(1)S=R2(cos θ-sin θ)sin θ,θ∈![]() ;(2)θ=
;(2)θ=![]() 时,S取得最大值
时,S取得最大值![]() R2.
R2.
【解析】
(1)分别过N,H作ND⊥OA于D,HE⊥OA于E,则HEDN为矩形,求出边长,即可求S关于θ的函数关系式;(2)利用二倍角公式、两角和的正弦函数化简函数的表达式为一个角的一个三角函数的形式,通过θ的范围求出S的最大值及相应的θ角.
(1)如图,过N作NP⊥OA于点P,过H作HE⊥OA于点E,∵∠AOB=![]() ,
,
∴OE=EH=NP=Rsin θ,OP=Rcos θ,
∴HN=EP=OP-OE=R(cos θ-sin θ),
∴S=HN·NP=R2(cos θ-sin θ)sin θ,θ∈![]() .
.
(2)S=R2(cos θsin θ-sin2θ)
=R2![]()
=![]() R2(sin 2θ+cos 2θ-1)
R2(sin 2θ+cos 2θ-1)
=![]() R2
R2![]() ,
,
∵θ∈![]() ,∴2θ+
,∴2θ+![]() ,
,
∴当2θ+![]() ,即θ=
,即θ=![]() 时,S取得最大值,且最大值为
时,S取得最大值,且最大值为![]() R2.
R2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】
袋中有形状和大小完全相同的四种不同颜色的小球,每种颜色的小球各有4个,分别编号为1,2,3,4.现从袋中随机取两个球.
(Ⅰ)若两个球颜色不同,求不同取法的种数;
(Ⅱ)在(1)的条件下,记两球编号的差的绝对值为随机变量X,求随机变量X的概率分布与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的三棱锥ABC﹣A1B1C1中,AA1⊥底面ABC,D,E分别是BC,A1B1的中点. 
(1)求证:DE∥平面ACC1A1;
(2)若AB⊥BC,AB=BC,∠ACB1=60°,求直线BC与平面AB1C所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的可导函数f(x)满足f′(x)+f(x)<0,设a=f(m﹣m2),b=e ![]() f(1),则a,b的大小关系是( )
f(1),则a,b的大小关系是( )
A.a>b
B.a<b
C.a=b
D.a,b的大小与m的值有关
查看答案和解析>>
科目:高中数学 来源: 题型:
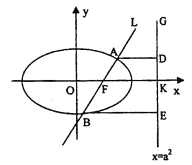
【题目】如图,已知直线![]() 的右焦点
的右焦点![]() ,且交椭圆
,且交椭圆![]() 于
于![]() 两点,点
两点,点![]() 在直线
在直线![]() 上的射影依次为点
上的射影依次为点![]() .
.
(Ⅰ)已知抛物线![]() 的焦点为椭圆
的焦点为椭圆![]() 的上顶点。
的上顶点。
①求椭圆![]() 的方程;
的方程;
②若直线![]() 交
交![]() 轴于点
轴于点![]() ,且
,且![]() ,当
,当![]() 变化时,求
变化时,求![]() 的值;
的值;
(Ⅱ)连接![]() ,试探索当
,试探索当![]() 变化时,直线
变化时,直线![]() 是否相交于一定点
是否相交于一定点![]() ?若交于定点
?若交于定点![]() ,请求出
,请求出![]() 点的坐标并给予证明;否则说明理由.
点的坐标并给予证明;否则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,圆C的参数方程 ![]() (φ为参数),以O为极点,x轴的非负半轴为极轴建立极坐标系.
(φ为参数),以O为极点,x轴的非负半轴为极轴建立极坐标系.
(1)求圆C的极坐标方程;
(2)直线l的极坐标方程是2ρsin(θ+ ![]() )=3
)=3 ![]() ,射线OM:θ=
,射线OM:θ= ![]() 与圆C的交点为O、P,与直线l的交点为Q,求线段PQ的长.
与圆C的交点为O、P,与直线l的交点为Q,求线段PQ的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com