
分析 (1)由焦点在y轴上,离心率$e=\frac{{\sqrt{2}}}{2}$,椭圆上的点到焦点的最短距离为$1-\frac{{\sqrt{2}}}{2}$,设椭圆$C:\frac{y^2}{a^2}+\frac{x^2}{b^2}=1\;(a>b>0)$,列出方程组求出a,b,由此能求出椭圆C的方程.
(2)当直线斜率不存在时:$m=±\frac{1}{2}$,当直线斜率存在时:设l与椭圆C交点为A(x1,y1),B(x2,y2),联立$\left\{{\begin{array}{l}{y=kx+m}\\{2{x^2}+{y^2}=1}\end{array}}\right.$,得(k2+2)x2+2kmx+(m2-1)=0,由此利用根的判别式、韦达定理、向量知识,结合已知条件能求出m的取值范围.
解答 解:(1)设椭圆$C:\frac{y^2}{a^2}+\frac{x^2}{b^2}=1\;(a>b>0)$,设c>0,c2=a2-b2,
由条件知$a-c=1-\frac{{\sqrt{2}}}{2},e=\frac{c}{a}=\frac{{\sqrt{2}}}{2}$,
解得$a=1,b=c=\frac{{\sqrt{2}}}{2}$,
故椭圆C的方程为:${y^2}+\frac{x^2}{{\frac{1}{2}}}=1$.
(2)当直线斜率不存在时:$m=±\frac{1}{2}$,
当直线斜率存在时,设l为y=kx+m,与椭圆C交点为A(x1,y1),B(x2,y2),
∴$\left\{{\begin{array}{l}{y=kx+m}\\{2{x^2}+{y^2}=1}\end{array}}\right.$,得(k2+2)x2+2kmx+(m2-1)=0
∴△=(2km)2-4(k2+2)(m2-1)=4(k2-2m2+2)>0,(*)
${x_1}+{x_2}=\frac{-2km}{{{k^2}+2}},{x_1}{x_2}=\frac{{{m^2}-1}}{{{k^2}+2}}$,
∵$\overline{AP}=3\overline{PB}$,∴-x1=3x2,∴$\left\{{\begin{array}{l}{{x_1}+{x_2}=-2{x_2}}\\{{x_1}{x_2}=-3x_2^2}\end{array}}\right.$,
消去x2,得$3{({x_1}+{x_2})^2}+4{x_1}{x_2}=0$,∴$3{(\frac{-2km}{{{k^2}+2}})^2}+4\frac{{{m^2}-1}}{{{k^2}+2}}=0$,
整理得4k2m2+2m2-k2-2=0,${m^2}=\frac{1}{4}$时,上式不成立,
${m^2}≠\frac{1}{4}$时,${k^2}=\frac{{2-2{m^2}}}{{4{m^2}-1}}$,
∴${k^2}=\frac{{2-2{m^2}}}{{4{m^2}-1}}≥0$时,∴$-1≤m<-\frac{1}{2}$或$\frac{1}{2}<m≤1$,
把${k^2}=\frac{{2-2{m^2}}}{{4{m^2}-1}}$代入(*)得$-1<m<-\frac{1}{2}$或$\frac{1}{2}<m<1$,
∴$-1<m<-\frac{1}{2}$或$\frac{1}{2}<m<1$.
综上m的取值范围为(-1,-$\frac{1}{2}$)∪($\frac{1}{2}$,1).
点评 本题考查椭圆方程的求法,考查实数的取值范围的求法,是中档题,解题时要认真审题,注意椭圆性质、根的判别式、韦达定理、向量知识的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,直线PA与圆切于点A,过P作直线与圆交于C、D两点,点B在圆上,且∠PAC=∠BCD.
如图,直线PA与圆切于点A,过P作直线与圆交于C、D两点,点B在圆上,且∠PAC=∠BCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
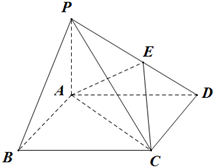 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AB=2,AD=4,E为线段PD上一动点(不含端点),记$\frac{PE}{PD}=λ$.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AB=2,AD=4,E为线段PD上一动点(不含端点),记$\frac{PE}{PD}=λ$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{15}{4}$ | C. | $\frac{17}{4}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π{b}^{2}}{2}$ | B. | $\frac{π{b}^{2}}{4}$ | C. | $\frac{π{b}^{2}}{8}$ | D. | $\frac{π{b}^{2}}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com