
分析 要对各个函数的定义域、值域逐一研究,其中对于函数y=sinx;y=tanx主要考察其值域,对于$y=x+\frac{1}{x}$主要考察单调性,对于$y=\frac{{{e^x}-{e^{-x}}}}{{{e^x}+{e^{-x}}}}$主要考察换元思想,对于y=x3+ax2+bx+1(-4≤x≤4),主要考察闭区间上的连续函数必有最大值和最小值这一性质.
解答 解:①∵y=|sinx|≤1,
∴函数y=|sinx|在区间R上有界.
②∵y=|x+$\frac{1}{x}$|≥2
∴函数y=|x+$\frac{1}{x}$|在区间{x|x≠0}上无界;
③∵y=|tanx|≥0
∴函数y=|tanx|在区间{x|x≠$\frac{π}{2}$+kπ,k∈Z}上无界;
④∵$y=\frac{{{e^x}-{e^{-x}}}}{{{e^x}+{e^{-x}}}}$;
令t=ex,t>0
则原式y=$\frac{{t}^{2}-1}{{t}^{2}+1}$=1-$\frac{2}{{t}^{2}+1}$∈(-1,1)
即值域为(-1,1)
∴存在M=1,对?x∈R,使得|f(x)|≤M恒成立,
∴④是有界的.
⑤∵y=x3+ax2+bx+1(-4≤x≤4),
∴y在区间[-4,4]上是连续的函数,故一定要最大值P和最小值Q,
设M=max{|P|,|Q|}
∴对?x∈D,?M∈R,使得|f(x)|≤M恒成立,
故⑤是有界的.
故本题答案为:①④⑤.
点评 本题是关于函数的定义域和值域方面的综合性问题,属于难题.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
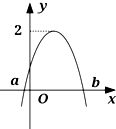 函数f(x)=Asin(2x+φ)(|φ|≤$\frac{π}{2}$,A>0)部分图象如图所示,且f(a)=f(b)=0,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有f(x1+x2)=$\sqrt{3}$,则( )
函数f(x)=Asin(2x+φ)(|φ|≤$\frac{π}{2}$,A>0)部分图象如图所示,且f(a)=f(b)=0,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有f(x1+x2)=$\sqrt{3}$,则( )| A. | f(x)在(-$\frac{5π}{12}$,$\frac{π}{12}$)上是减函数 | B. | f(x)在(-$\frac{5π}{12}$,$\frac{π}{12}$)上是增函数 | ||
| C. | f(x)在($\frac{π}{3}$,$\frac{5π}{6}$)上是减函数 | D. | f(x)在($\frac{π}{3}$,$\frac{5π}{6}$)上是增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x2-1 | B. | f(x)=2x+1 | ||
| C. | f(x)=$\left\{\begin{array}{l}{{x}^{2}+1(x>1)}\\{{x}^{2}-1(x≤1)}\end{array}\right.$ | D. | f(x)=2x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com