
分析 (1)把a=1,b=1代入函数解析式,在函数解析式中,然后分类去绝对值,求解关于x 的方程后得答案;
(2)在b<0的前提下,在x∈(0,1]时,把不等式恒成立转化为$x+\frac{b}{x}<a<x-\frac{b}{x}$,由单调性求得左侧函数的最大值和右侧函数的最小值得a的取值范围.
解答 解:(1)当a=1,b=1时,f(x)=x|x-1|+1,
由$f(x)=\frac{5}{4}$,得x|x-1|+1=$\frac{5}{4}$,
即x|x-1|=$\frac{1}{4}$
若x≥1时,方程等价为x2-x=$\frac{1}{4}$,即4x2-4x-1=0,得x=$\frac{1+\sqrt{2}}{2}$或x=$\frac{1-\sqrt{2}}{2}$(舍),
若x<1时,方程等价为-x2+x=$\frac{1}{4}$,即4x2-4x+1=0,得x=$\frac{1}{2}$,
综上x=$\frac{1+\sqrt{2}}{2}$或x=$\frac{1}{2}$;
(2)当x∈(0,1],此时原不等式变为$|x-a|<\frac{-b}{x}$,
即$x+\frac{b}{x}<a<x-\frac{b}{x}$,
故${(x+\frac{b}{x})_{max}}<a<{(x-\frac{b}{x})_{min}},x∈({0,1}]$,
∵b<0,
∴函数$g(x)=x+\frac{b}{x}$在(0,1]上单调递增,
∴${(x+\frac{b}{x})_{max}}=g(1)=1+b$,
令h(x)=x-$\frac{b}{x}$,则h(x)在(0,$\sqrt{-b}$) 上单调递减,[$\sqrt{-b}$,+∞)单调递增
当b<-1时,h(x)=x-$\frac{b}{x}$在0<x≤1上单调递减;
∴a<hmin(x)=h(1)=1-b,∴1+b<a<1-b.
而-1≤b<0时,h(x)=x-$\frac{b}{x}$≥2$\sqrt{x•(-\frac{b}{x})}$=2$\sqrt{-b}$.
∴a<hmin(x)=2 $\sqrt{-b}$.
∴1+b<a<2 $\sqrt{-b}$,
∴此时a的取值范围是(1+b,2$\sqrt{-b}$ ).
点评 本题考查恒成立问题,体现了分类讨论的数学思想方法和数学转化思想方法,综合性较强,运算量较大,属有一定难度题目.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 5 | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
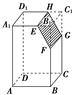 如图,记长方体ABCD-A1B1C1D1被平行于棱B1C1的平面EFGH截去右上部分后剩下的几何体为Ω,则下列结论中不正确的是( )
如图,记长方体ABCD-A1B1C1D1被平行于棱B1C1的平面EFGH截去右上部分后剩下的几何体为Ω,则下列结论中不正确的是( )| A. | EH∥FG | B. | 四边形EFGH是平行四边形 | ||
| C. | Ω是棱柱 | D. | Ω是棱台 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<e} | B. | {x|0≤x≤e} | C. | {x|x≤e} | D. | {x|x>e} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com