
分析 (1)设c=t,则a=2t,$b=\sqrt{3}t$,推导出点P为短轴端点,从而得到t=1,由此能求出椭圆的方程.
(2)设直线AB的方程为x=ty+1,联立$\left\{\begin{array}{l}x=ty+1\\ \frac{x^2}{4}+\frac{y^2}{3}=1\end{array}\right.$,得(3t2+4)y2+6ty-9=0,由此利用韦达定理、向量知识、直线方程、圆的性质、椭圆性质,结合已知条件能推导出以PQ为直径的圆恒过定点(1,0)和(7,0).
解答 (本小题满分12分)
解:(1)∵椭圆的离心率为$\frac{1}{2}$,不妨设c=t,a=2t,即$b=\sqrt{3}t$,其中t>0,
又△F1PF2内切圆面积取最大值$\frac{π}{3}$时,半径取最大值为$r=\frac{{\sqrt{3}}}{3}$,
∵${S_{△{F_1}P{F_2}}}=\frac{r}{2}•{C_{△{F_1}P{F_2}}}$,${C_{△{F_1}P{F_2}}}$为定值,
∴${S_{△{F_1}P{F_2}}}$也取得最大值,即点P为短轴端点,
∴$\frac{1}{2}•2c•b=\frac{r}{2}•(2a+2c)$,$\frac{1}{2}•2t•\sqrt{3}t=\frac{1}{2}•\frac{{\sqrt{3}}}{3}•(4t+2t)$,解得t=1,
∴椭圆的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.(4分)
(2)设直线AB的方程为x=ty+1,A(x1,y1),B(x2,y2),
联立$\left\{\begin{array}{l}x=ty+1\\ \frac{x^2}{4}+\frac{y^2}{3}=1\end{array}\right.$,得(3t2+4)y2+6ty-9=0,
则${y_1}+{y_2}=\frac{-6t}{{3+4{t^2}}}$,${y_1}{y_2}=\frac{-9}{{3+4{t^2}}}$,
直线AA1的方程为$y=\frac{y_1}{{{x_1}-(-2)}}(x-(-2))$,
直线BA1的方程为$y=\frac{y_2}{{{x_2}-(-2)}}(x-(-2))$,
则$P(4,\frac{{6{y_1}}}{{{x_1}+2}})$,$Q(4,\frac{{6{y_2}}}{{{x_2}+2}})$,
假设PQ为直径的圆是否恒过定点M(m,n),
则$\overrightarrow{MP}=(4-m,\frac{{6{y_1}}}{{{x_1}+2}}-n)$,$\overrightarrow{MQ}=(4-m,\frac{{6{y_2}}}{{{x_2}+2}}-n)$,
$\overrightarrow{MP}•\overrightarrow{MQ}={(4-m)^2}+(\frac{{6{y_1}}}{{{x_1}+2}}-n)(\frac{{6{y_2}}}{{{x_2}+2}}-n)=0$,
即$\overrightarrow{MP}•\overrightarrow{MQ}={(4-m)^2}+(\frac{{6{y_1}}}{{t{y_1}+3}}-n)(\frac{{6{y_2}}}{{t{y_2}+3}}-n)=0$,
即$\frac{{(36-12nt){y_1}{y_2}-18n({y_1}+{y_2})}}{{{t^2}{y_1}{y_2}+3t({y_1}+{y_2})+9}}+{n^2}+{(4-m)^2}=0$,
$\frac{(36-12nt)(-9)-18n(-6t)}{{-9{t^2}+3t(-6t)+9(3{t^2}+4)}}+{n^2}+{(4-m)^2}=0$,即6nt-9+n2+(4-m)2=0,
若PQ为直径的圆是否恒过定点M(m,n),即不论t为何值时,$\overrightarrow{MP}•\overrightarrow{MQ}=0$恒成立,
∴n=0,m=1或m=7.
∴以PQ为直径的圆恒过定点(1,0)和(7,0).(12分)
点评 本小题主要考查直线与圆锥曲线的综合应用能力,具体涉及到椭圆方程的求法,直线与圆锥曲线的相关知识,以及恒过定点问题.本小题对考生的化归与转化思想、运算求解能力都有很高要求.


 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
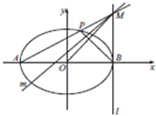 如图,在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,且过点(1,$\frac{3}{2}$),
如图,在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,且过点(1,$\frac{3}{2}$),查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
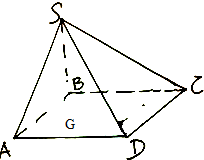 如图,已知四棱锥S-ABCD是底面边长为$2\sqrt{3}$的菱形,且$∠BAD=\frac{π}{3}$,若$∠ASC=\frac{π}{2}$,SB=SD
如图,已知四棱锥S-ABCD是底面边长为$2\sqrt{3}$的菱形,且$∠BAD=\frac{π}{3}$,若$∠ASC=\frac{π}{2}$,SB=SD查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 5 | C. | 4 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com