
分析 利用换元法,将不等式恒成立问题转化为一元二次不等式恒成立,讨论判别式△与对称性的关系进行求解即可.
解答 解:由acos2x+cosx≥-1得a(2cos2x-1)+cosx+1≥0,
令cosx=t,t∈[-1,1],
则原命题可转换为(2t2-1)a+t+1≥0恒成立
则2at2+t+1-a≥0恒成立,令f(t)=2at2+t+1-a
首先f(-1)=2a-1+1-a=a≥0,f(1)=2a+2-a=a+2≥0,得a≥-2.
此时a≥0,
若△≤0,得1-4×2a×(1-a)≤0,即8a2-8a+1≤0解得$\frac{2-\sqrt{2}}{4}$≤a≤$\frac{2+\sqrt{2}}{4}$,
∵a≥0,$\frac{2-\sqrt{2}}{4}$≤a≤$\frac{2+\sqrt{2}}{4}$,∴$\frac{2-\sqrt{2}}{4}$≤a≤$\frac{2+\sqrt{2}}{4}$
若判别式△>0,即a>$\frac{2+\sqrt{2}}{4}$,
此时函数的最小值为$\frac{-4×2{a}^{2}-1}{4×2a}$=$\frac{-1-8{a}^{2}}{8a}$>0恒成立,
此时不等式无解,
综上a的范围是[$\frac{2-\sqrt{2}}{4}$,$\frac{2+\sqrt{2}}{4}$],
故答案为:[$\frac{2-\sqrt{2}}{4}$,$\frac{2+\sqrt{2}}{4}$]
点评 本题主要考查不等式恒成立问题,利用换元法转化为一元二次不等式,利用一元二次不等式和一元二次函数之间的关系是解决本题的关键.综合性较强,有一定的难度.


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
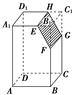 如图,记长方体ABCD-A1B1C1D1被平行于棱B1C1的平面EFGH截去右上部分后剩下的几何体为Ω,则下列结论中不正确的是( )
如图,记长方体ABCD-A1B1C1D1被平行于棱B1C1的平面EFGH截去右上部分后剩下的几何体为Ω,则下列结论中不正确的是( )| A. | EH∥FG | B. | 四边形EFGH是平行四边形 | ||
| C. | Ω是棱柱 | D. | Ω是棱台 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 16 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com