
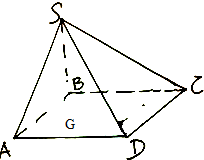
 如图,已知四棱锥S-ABCD是底面边长为$2\sqrt{3}$的菱形,且$∠BAD=\frac{π}{3}$,若$∠ASC=\frac{π}{2}$,SB=SD
如图,已知四棱锥S-ABCD是底面边长为$2\sqrt{3}$的菱形,且$∠BAD=\frac{π}{3}$,若$∠ASC=\frac{π}{2}$,SB=SD分析 (1)证明BD⊥平面SAC,由∠ASC=$\frac{π}{2}$可知S的轨迹为与平面ABCD垂直的平面SAC内以AC为直径的半圆上,从而求出S到平面ABCD的距离的取值范围,从而求出棱锥的体积的范围;
(2)以E为原点建立空间直角坐标系,求出$\overrightarrow{AS}$和平面SCD的法向量$\overrightarrow{n}$,利用$\overrightarrow{AS}$与$\overrightarrow{n}$的夹角(或补角)与所求线面角互余即可求出直线SA与平面SCD夹角的余弦值.
解答 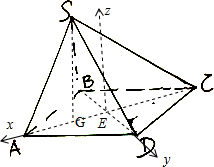 解:(1)连结AC、BD,设交点为E,连结SE,
解:(1)连结AC、BD,设交点为E,连结SE,
∵四边形ABCD为菱形,∴AC⊥BD,
∵E为BD中点,SB=SD,
∴BD⊥SE,又BD⊥AC,SE?平面SAC,AC?平面SAC,AC∩SE=E,
∴BD⊥面SAC.
又∵$∠ASC=\frac{π}{2}$,∴点S在平面SAC内以AC为直径的圆上运动,
设S到平面ABCD的距离为h,则0<h≤$\frac{1}{2}AC$=2$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=3.
又S菱形ABCD=2×$\frac{\sqrt{3}}{4}×(2\sqrt{3})^{2}$=6$\sqrt{3}$,
∴当h=3时,四棱锥S-ABCD的体积取得最大值.最大体积为$\frac{1}{3}×6\sqrt{3}×3$=6$\sqrt{3}$.
∴四棱锥S-ABCD的体积的取值范围是$(0,6\sqrt{3}]$.
(2)∵G为△ABD的重心,∴AG=$\frac{2}{3}AE$=2,∴CG=4,
∵SG2=AG•GC,∴SG=2$\sqrt{2}$,
E为原点,以AC为x轴,BD为y轴,平面ABCD的垂线为z轴建立空间直角坐标系,如图所示:
则S(1,0,2$\sqrt{2}$),D(0,$\sqrt{3}$,0),A(3,0,0),C(-3,0,0),
∴$\overrightarrow{AS}$=(-2,0,2$\sqrt{2}$),$\overrightarrow{CD}$=(3,$\sqrt{3}$,0),$\overrightarrow{DS}$=(1,-$\sqrt{3}$,2$\sqrt{2}$),
设平面SDC法向量$\overrightarrow{n}$=(x,y,z),则$\overrightarrow{n}•\overrightarrow{CD}=0$,$\overrightarrow{n}•\overrightarrow{DS}=0$,
∴$\left\{\begin{array}{l}{3x+\sqrt{3}y=0}\\{x-\sqrt{3}y+2\sqrt{2}z=0}\end{array}\right.$,令x=1得$\overrightarrow{n}$=(1,-$\sqrt{3}$,-$\sqrt{2}$),
∴cos<$\overrightarrow{AS},\overrightarrow{n}$>=$\frac{\overrightarrow{AS}•\overrightarrow{n}}{|\overrightarrow{AS}||\overrightarrow{n}|}$=$\frac{-6}{2\sqrt{3}•\sqrt{6}}$=-$\frac{\sqrt{2}}{2}$.
设直线SA与平面SCD夹角为$\overrightarrow{θ}$,
则$sinθ=|cos<\overrightarrow{AS}•\overrightarrow n>|=\frac{{\sqrt{2}}}{2}$,∴$cosθ=\sqrt{1-{{(\frac{{\sqrt{2}}}{2})}^2}}=\frac{{\sqrt{2}}}{2}$.
点评 本题考查了线面垂直的判定,棱锥的体积计算,线面角的计算,属于中档题.


 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<e} | B. | {x|0≤x≤e} | C. | {x|x≤e} | D. | {x|x>e} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | $\frac{3}{8}$ | C. | $-3或\frac{3}{8}$ | D. | $3或-\frac{3}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{e}$ | D. | $\frac{1}{2e}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com