
分析 (1)根据椭圆定义得出a=2,把A点坐标代入椭圆方程即可求出b,从而得出椭圆方程;
(2)根据三角形相似及P点纵坐标的范围即可求出GH的最小值,求出PF1的距离及所在直线方程,设T(2cosθ,sinθ),利用距离公式求出最大距离即可得出三角形的最大面积.
解答 解:(1)∵|F1P|+|F2P|=2a=4,∴a=2,
把A(c,$\frac{1}{2}$)代入椭圆方程得$\frac{{c}^{2}}{4}+\frac{1}{4{b}^{2}}=1$,又c2=a2-b2=4-b2,
∴b2=1,
∴椭圆方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$.
(2)F1F2=2c=2$\sqrt{{a}^{2}-{b}^{2}}$=2$\sqrt{3}$,
设P(x0,y0),∵△PF1F2∽△PGH,
∴$\frac{GH}{{F}_{1}{F}_{2}}$=$\frac{3-{y}_{0}}{{y}_{0}}$=$\frac{3}{{y}_{0}}$-1,∴GH=2$\sqrt{3}$($\frac{3}{{y}_{0}}$-1),
∵0<y0≤1,∴当y0=1时,GH取得最小值4$\sqrt{3}$.
当y0=1时,P(0,1),F1(-$\sqrt{3}$,0),∴PF1=2,直线PF1的方程为$\sqrt{3}$x-3y+3=0,
设T(2cosθ,sinθ),则T到直线PF1的距离d=$\frac{|2\sqrt{3}cosθ-3sinθ+3|}{2\sqrt{3}}$=$\frac{|\sqrt{21}cos(θ+φ)+3|}{2\sqrt{3}}$,
∴当cos(θ+φ)=1时,d取得最大值$\frac{\sqrt{7}+\sqrt{3}}{2}$,
∴△TPF1面积的最大值为$\frac{1}{2}×2×\frac{\sqrt{7}+\sqrt{3}}{2}$=$\frac{\sqrt{7}+\sqrt{3}}{2}$.
点评 本题考查令椭圆的性质,直线与椭圆的位置关系,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{8}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{{-3+4\sqrt{3}}}{2}$,$\frac{{-4+3\sqrt{3}}}{2}$) | B. | ($\frac{{-3+4\sqrt{3}}}{2}$,$\frac{{-4-3\sqrt{3}}}{2}$) | C. | ($\frac{{-4+3\sqrt{3}}}{2}$,$\frac{{-3-4\sqrt{3}}}{2}$) | D. | ($\frac{{-4-3\sqrt{3}}}{2}$,$\frac{{-3+4\sqrt{3}}}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
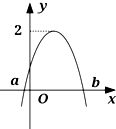 函数f(x)=Asin(2x+φ)(|φ|≤$\frac{π}{2}$,A>0)部分图象如图所示,且f(a)=f(b)=0,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有f(x1+x2)=$\sqrt{3}$,则( )
函数f(x)=Asin(2x+φ)(|φ|≤$\frac{π}{2}$,A>0)部分图象如图所示,且f(a)=f(b)=0,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有f(x1+x2)=$\sqrt{3}$,则( )| A. | f(x)在(-$\frac{5π}{12}$,$\frac{π}{12}$)上是减函数 | B. | f(x)在(-$\frac{5π}{12}$,$\frac{π}{12}$)上是增函数 | ||
| C. | f(x)在($\frac{π}{3}$,$\frac{5π}{6}$)上是减函数 | D. | f(x)在($\frac{π}{3}$,$\frac{5π}{6}$)上是增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
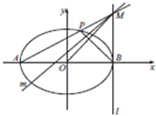 如图,在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,且过点(1,$\frac{3}{2}$),
如图,在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,且过点(1,$\frac{3}{2}$),查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
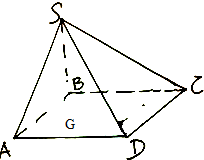 如图,已知四棱锥S-ABCD是底面边长为$2\sqrt{3}$的菱形,且$∠BAD=\frac{π}{3}$,若$∠ASC=\frac{π}{2}$,SB=SD
如图,已知四棱锥S-ABCD是底面边长为$2\sqrt{3}$的菱形,且$∠BAD=\frac{π}{3}$,若$∠ASC=\frac{π}{2}$,SB=SD查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com