
分析 (1)求出M,P坐标之间的关系,利用代入法求动点M的轨迹E的方程;
(2)证明$\overrightarrow{QF}$•$\overrightarrow{RF}$=0,即可证明结论.
解答 (1)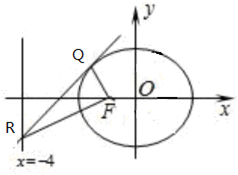 解:设M的坐标为(x,y),P的坐标为(xP,yP),
解:设M的坐标为(x,y),P的坐标为(xP,yP),
由已知得xP=x,yP=$\frac{2}{\sqrt{3}}$y,
∵点P在圆上,∴x2+($\frac{2}{\sqrt{3}}$y)2=4,即$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1,
∴点M的轨迹方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.(4分)
(2)证明:由$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$得(4k2+3)x2+8kmx+4m2-12=0.
如图,设点Q的坐标为(x0,y0),依题意m≠0,
由△=0可得4k2+3=m2,(6分)
此时x0=-$\frac{4k}{m}$,y0=$\frac{3}{m}$,
∴Q(-$\frac{4k}{m}$,$\frac{3}{m}$),
由$\left\{\begin{array}{l}{y=kx+m}\\{x=-4}\end{array}\right.$解得y=-4k+m,∴R(-4,-4k+m) (9分)
由F(-1,0),$\overrightarrow{QF}$=($\frac{4k}{m}$-1,-$\frac{3}{m}$),$\overrightarrow{RF}$=(3,4k-m)
∴$\overrightarrow{QF}$•$\overrightarrow{RF}$=3($\frac{4k}{m}$-1)-$\frac{3}{m}$•(4k-m)=0,
∴QF⊥RF.
∴以QR为直径的圆过定点F.(12分)
点评 本题考查了圆锥曲线的定义与性质及向量的应用,属于中档题.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com