
| A. | 2 | B. | $\frac{15}{4}$ | C. | $\frac{17}{4}$ | D. | 4 |
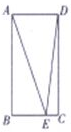
分析 以B为坐标原点,BC所在直线为x轴建立直角坐标系,利用坐标表示$\overrightarrow{AE}$•$\overrightarrow{DE}$,计算它的最小值.
解答 解:如图所示,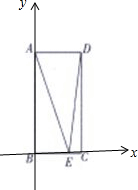
以B为坐标原点,BC所在直线为x轴建立直角坐标系,
则A(0,2),D(1,2),E(x,0),
所以$\overrightarrow{AE}$•$\overrightarrow{DE}$=(x,-2)•(x-1,-2)
=x2-x+4
=${(x-\frac{1}{2})}^{2}$+$\frac{15}{4}$,
因为E为线段BC上的点,所以x∈[0,1],
所以当$x=\frac{1}{2}$时,$\overrightarrow{AE}\;•\;\overrightarrow{DE}$取得最小值$\frac{15}{4}$.
故选:B.
点评 本题考查了平面向量数量积的定义与应用问题,是基础题目.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:选择题
| A. | cos2θ≤x≤1 | B. | -1≤x≤-cos2θ | C. | -cos2θ≤x≤1 | D. | -1≤x≤cos2θ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
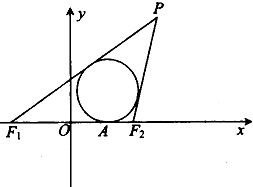 在平面直角坐标系中,已知△PF1F2的两个顶点为F1(-$\sqrt{2}$a,0),F2($\sqrt{2}$a,0)(a>0),顶点P在曲线C上运动,△PF1F2的内切圆与x轴的切点为A,满足|AF1|-|AF2|=2a.
在平面直角坐标系中,已知△PF1F2的两个顶点为F1(-$\sqrt{2}$a,0),F2($\sqrt{2}$a,0)(a>0),顶点P在曲线C上运动,△PF1F2的内切圆与x轴的切点为A,满足|AF1|-|AF2|=2a.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
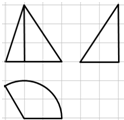
| A. | $\frac{2π}{3}$ | B. | $\frac{4π}{3}$ | C. | $\frac{14π}{3}$ | D. | $\frac{16π}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | an=2n-3 | B. | an=2n-4 | C. | an=3-3n | D. | an=2n-5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com