
【题目】如图,已知正四面体D﹣ABC(所有棱长均相等的三棱锥),P、Q、R分别为AB、BC、CA上的点,AP=PB, ![]() =
= ![]() =2,分别记二面角D﹣PR﹣Q,D﹣PQ﹣R,D﹣QR﹣P的平面角为α、β、γ,则( )
=2,分别记二面角D﹣PR﹣Q,D﹣PQ﹣R,D﹣QR﹣P的平面角为α、β、γ,则( )
A.γ<α<β
B.α<γ<β
C.α<β<γ
D.β<γ<α
【答案】B
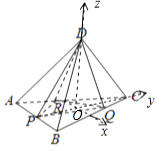
【解析】解法一:如图所示,建立空间直角坐标系.设底面△ABC的中心为O.
不妨设OP=3.则O(0,0,0),P(0,﹣3,0),C(0,﹣6,0),D(0,0,6 ![]() ),
),
Q ![]() ,R
,R ![]() ,
,![]() =
= ![]() ,
, ![]() =(0,3,6
=(0,3,6 ![]() ),
), ![]() =(
=( ![]() ,5,0),
,5,0), ![]() =
= ![]() ,
,![]() =
= ![]() .
.
设平面PDR的法向量为 ![]() =(x,y,z),则
=(x,y,z),则 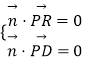 ,可得
,可得 ![]() ,
,
可得 ![]() =
= ![]() ,取平面ABC的法向量
,取平面ABC的法向量 ![]() =(0,0,1).
=(0,0,1).
则cos ![]() =
= ![]() =
= ![]() ,取α=arccos
,取α=arccos ![]() .
.
同理可得:β=arccos ![]() .γ=arccos
.γ=arccos ![]() .
.
∵ ![]() >
> ![]() >
> ![]() .
.
∴α<γ<β.
解法二:如图所示,连接OD,OQ,OR,过点O发布作垂线:OE⊥DR,OF⊥DQ,OG⊥QR,垂足分别为E,F,G,连接PE,PF,PG.
设OP=h.
则cosα= ![]() =
= ![]() =
= ![]() .
.
同理可得:cosβ= ![]() =
= ![]() ,cosγ=
,cosγ= ![]() =
= ![]() .
.
由已知可得:OE>OG>OF.
∴cosα>cosγ>cosβ,α,β,γ为锐角.
∴α<γ<β.
故选:B.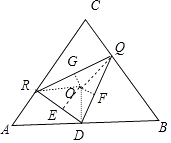



科目:高中数学 来源: 题型:
【题目】设 ![]() ,
, ![]() 为非零向量,则“存在负数λ,使得
为非零向量,则“存在负数λ,使得 ![]() =λ
=λ ![]() ”是
”是 ![]()
![]() <0”的( )
<0”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=excosx﹣x.(13分)
(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)求函数f(x)在区间[0, ![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正三棱柱中,AB=2,由顶点B沿棱柱侧面经过棱![]() 到顶点C1的最短路线与棱
到顶点C1的最短路线与棱![]() 的交点记为M,求:
的交点记为M,求:
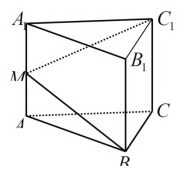
(Ⅰ)三棱柱的侧面展开图的对角线长.
(Ⅱ)该最短路线的长及![]() 的值.
的值.
(Ⅲ)平面![]() 与平面ABC所成二面角(锐二面角)
与平面ABC所成二面角(锐二面角)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图所示,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成的角为60°.

(1)求证:AC⊥平面BDE;
(2)求二面角F-BE-D的余弦值;
(3)设点M是线段BD上一个动点,试确定点M的位置,使得AM∥平面BEF,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com