
分析 求出正四面体的底面面积以及高,即可求解正四面体的体积.
解答  解:作正四面体的高SO,垂足为O,则O为等边三角形ABC的中心,
解:作正四面体的高SO,垂足为O,则O为等边三角形ABC的中心,
∵AB=a,∴AD=$\frac{\sqrt{3}}{2}$a,AO=$\frac{2}{3}$AD=$\frac{\sqrt{3}}{3}$a,
∴SO=$\sqrt{A{S}^{2}-A{O}^{2}}$=$\frac{\sqrt{6}}{3}$a,
∴正四面体的体积V=$\frac{1}{3}$S△ABC•SO=$\frac{1}{3}×\frac{\sqrt{3}}{4}{a}^{2}×\frac{\sqrt{6}}{3}a$=$\frac{\sqrt{2}}{12}$a3.
故答案为:$\frac{{\sqrt{2}}}{12}{a^3}$.
点评 本题考查几何体的体积的求法,求解正四面体的高是解题的关键,属于中档题.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | -2 | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 496 | B. | 33 | C. | 31 | D. | $\frac{31}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)=\sqrt{x^2}\;\;,\;\;g(x)=x$ | B. | $f(x)=\sqrt{x^2}\;,\;\;g(t)=\left\{\begin{array}{l}t,t≥0\\-t,t<0\end{array}\right.$ | ||
| C. | $f(x)=\root{3}{x^3}\;\;,\;\;g(x)=|x|$ | D. | $f(t)=t\;,\;\;g(x)=\frac{x^2}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
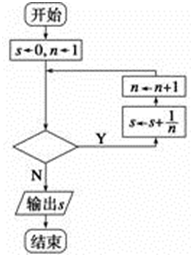
| A. | n>12 | B. | n<12 | C. | n<13 | D. | n>13 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com