


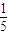

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:044
如图所示,在边长为l的等边△ABC中,⊙O1为△ABC的内切圆.⊙O2与⊙O1外切,且与AB、BC相切,…,⊙On+1与⊙On外切,且与AB、BC相切,如此无限继续下去.记⊙On的面积为an(n∈N*).
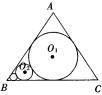
(1)证明{an}是等比数列;
(2)求![]() (a1+a2+…+an)的值
(a1+a2+…+an)的值
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
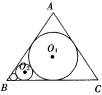
(1)证明{an}是等比数列;
(2)求![]() (a1+a2+…+an)的值
(a1+a2+…+an)的值
查看答案和解析>>
科目:高中数学 来源:2014届山东省高二下学期3月月考理科数学试卷(解析版) 题型:选择题
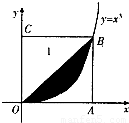
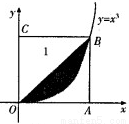
如图所示,在边长为l的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )
A.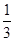 B.
B.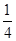 C.
C.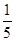 D.
D.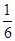
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com