
分析 (1)由b1=1,bn+1=$\frac{{b}_{n}}{1+2{b}_{n}}$,分别令n=1,2,3,即可得出,猜想bn=$\frac{1}{2n-1}$,
(2)利用数学归纳法证明即可,
(3)先求出cn=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),裂项求和即可.
解答 解:(1)b2=$\frac{{b}_{1}}{1+2{b}_{1}}$=$\frac{1}{1+2}$=$\frac{1}{3}$,b3=$\frac{\frac{1}{3}}{1+\frac{2}{3}}$=$\frac{1}{5}$,b4=$\frac{\frac{1}{5}}{1+\frac{2}{5}}$=$\frac{1}{7}$,可以猜想bn=$\frac{1}{2n-1}$
(2)证明:①当n=1时,猜想显然成立;
②假设当n=k(k∈N+)时猜想成立,
即bk=$\frac{1}{2k-1}$,则bk+1=$\frac{\frac{1}{2k-1}}{1+\frac{2}{2k-1}}$=$\frac{1}{2k+1}$=$\frac{1}{2(k+1)-1}$,
故当然n=k+1时猜想成立,
由①②可知,猜想成立;
(3)cn=bnbn+1=$\frac{1}{2n-1}$•$\frac{1}{2n+1}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),
故Tn=$\frac{1}{2}$$\sum_{i=1}^{n}$($\frac{1}{2i-1}$-$\frac{1}{2i+1}$)=$\frac{1}{2}$(1-$\frac{1}{2n+1}$)=$\frac{n}{2n+1}$.
点评 本题考查了数学归纳法、递推公式、数列的通项公式,考查了猜想归纳能力与计算能力,属于中档题.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:解答题
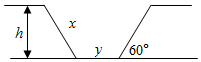 某地兴修水利开建一条水渠,其断面为等腰梯形,腰与水平线的夹角为60°,要求湿透周长(即断面与水接触的边界长度)为定值l.问渠深h为多少时,可使水流量最大?最大水流量是多少?
某地兴修水利开建一条水渠,其断面为等腰梯形,腰与水平线的夹角为60°,要求湿透周长(即断面与水接触的边界长度)为定值l.问渠深h为多少时,可使水流量最大?最大水流量是多少?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
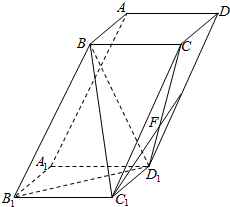 如图,四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,且B1C1=$\sqrt{2}$,BB1=BC1=BD1=$\sqrt{5}$.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,且B1C1=$\sqrt{2}$,BB1=BC1=BD1=$\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\sqrt{e}$) | B. | ($\sqrt{e}$,+∞) | C. | (-∞,e) | D. | (e,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x-1 | B. | f(x)=x${\;}^{\frac{1}{2}}$ | C. | f(x)=x2 | D. | f(x)=x3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2 个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com