
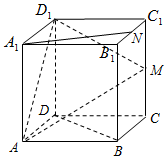
 如图边长为2的正方体ABCD-A1B1C1D1中,M,N分别是CC1,B1C1的中点,
如图边长为2的正方体ABCD-A1B1C1D1中,M,N分别是CC1,B1C1的中点,分析 (Ⅰ)以D为原点,DA、DC、DD1为轴建立空间直角坐标系,利用向量法能证明A1N∥平面AMD1.
(Ⅱ)求出平面ADD1的一个法向量和平面AMD1的法向量,利用向量法能求出二面角M-AD1-D的余弦值.
解答 证明:(Ⅰ)以D为原点,DA、DC、DD1为轴建立如图直角坐标系.…(1分)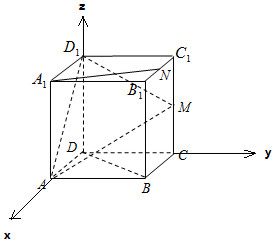
则A1(2,0,2),N(1,2,2),M(0,2,1),A(2,0,0),D1(0,0,2).
$\overrightarrow{{A_1}N}=(-1,2,0),\overrightarrow{AM}=(-2,2,1),\overrightarrow{A{D_1}}=(-2,0,2)$.…(2分)
设平面AMD1的法向量是$\overrightarrow n=(x,y,z)$.
则$\left\{\begin{array}{l}-2x+2y+z=0\\-2x+2z=0\end{array}\right.$.…(3分)取x=1,得$\overrightarrow n=(1,\frac{1}{2},1)$.…(4分)
所以$\overrightarrow{{A_1}N}•\overrightarrow n=(-1)×1+2×\frac{1}{2}=0$,即$\overrightarrow{{A_1}N}⊥\overrightarrow n$.…(5分)
又A1N?平面AMD1.∴A1N∥平面AMD1.…(6分)
解:(Ⅱ)平面ADD1的一个法向量为$\overrightarrow m=(0,1,0)$,…(8分)
平面AMD1的法向量是$\overrightarrow n=(1,\frac{1}{2},1)$.
由(Ⅰ)得$cos<\overrightarrow n,\overrightarrow m>=\frac{\overrightarrow n•\overrightarrow m}{|\overrightarrow n|•|\overrightarrow m|}=\frac{{\frac{1}{2}}}{{\sqrt{{1^2}+{1^2}+{{(\frac{1}{2})}^2}}}}=\frac{1}{3}$.…(11分)
由图形得二面角M-AD1-D的平面角是锐角,
所以二面角M-AD1-D的余弦值是$\frac{1}{3}$.…(12分)
点评 本题考查线面平行的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知四棱柱ABC-A1B1C1D1的底面是边长为2的菱形,且∠BAD=$\frac{π}{3}$,AA1⊥平面ABCD,设E为CD的中点
已知四棱柱ABC-A1B1C1D1的底面是边长为2的菱形,且∠BAD=$\frac{π}{3}$,AA1⊥平面ABCD,设E为CD的中点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点$({\sqrt{2},\sqrt{2}})$,直线l:y=kx(k≠0)与椭圆E交于P、A两点,过点P作PC⊥x轴,垂足为C点,直线AC交椭圆E与另一点B,当$k=\sqrt{2}$时,椭圆E的右焦点到直线l的距离为$\sqrt{2}$.
如图所示,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点$({\sqrt{2},\sqrt{2}})$,直线l:y=kx(k≠0)与椭圆E交于P、A两点,过点P作PC⊥x轴,垂足为C点,直线AC交椭圆E与另一点B,当$k=\sqrt{2}$时,椭圆E的右焦点到直线l的距离为$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在边长为4的菱形ABCD中,∠BAD=60°,DE⊥AB于点E,将△ADE沿DE折起到△A1DE的位置,使A1E⊥EB.
如图,在边长为4的菱形ABCD中,∠BAD=60°,DE⊥AB于点E,将△ADE沿DE折起到△A1DE的位置,使A1E⊥EB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
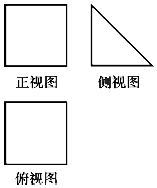 一块硬质材料的三视图如图所示,正视图和俯视图都是边长为10cm的正方形,将该木料切削、打磨,加工成球,则能得到的最大球的半径最接近( )
一块硬质材料的三视图如图所示,正视图和俯视图都是边长为10cm的正方形,将该木料切削、打磨,加工成球,则能得到的最大球的半径最接近( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com