
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
分析 由题意画出图形,通过分割补形,求出B到底面ACD的距离,代入体积公式求解.
解答 解:如图,
在AC上取E,使AE=2,在AD上取F,使AF=2,连接BE、BF、EF,
则四面体B-AEF为正四面体,过B作BO⊥平面AEF,垂足为O,
连接AO并延长,交EF于G,则AG=$\sqrt{3}$,AO=$\frac{2\sqrt{3}}{3}$,
∴BO=$\sqrt{{2}^{2}-(\frac{2\sqrt{3}}{3})^{2}}=\frac{2\sqrt{6}}{3}$.
${S}_{△ACD}=\frac{1}{2}AC×AD×sin60°=\frac{1}{2}×3×4×\frac{\sqrt{3}}{2}$=$3\sqrt{3}$.
∴${V}_{B-ACD}=\frac{1}{3}×3\sqrt{3}×\frac{2\sqrt{6}}{3}=2\sqrt{2}$.
故选:A.
点评 本题考查棱柱、棱锥、棱台的体积,考查空间想象能力和逻辑思维能力,是中档题.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源:2017届湖南衡阳县四中高三9月月考数学(文)试卷(解析版) 题型:选择题
下列命题中正确的是( )
A.若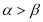 ,则
,则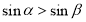 ;
;
B.命题:“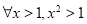 ”的否定是“
”的否定是“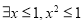 ”;
”;
C.直线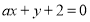 与
与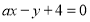 垂直的充要条件为
垂直的充要条件为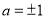 ;
;
D.“若 ,则
,则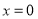 或
或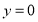 ”的逆否命题为“若
”的逆否命题为“若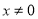 或
或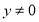 ,则
,则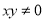 ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
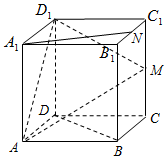 如图边长为2的正方体ABCD-A1B1C1D1中,M,N分别是CC1,B1C1的中点,
如图边长为2的正方体ABCD-A1B1C1D1中,M,N分别是CC1,B1C1的中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在三棱锥A-BCD中,平面ABC⊥平面BCD,△BAC与△BCD均为等腰直角三角形,且∠BAC=∠BCD=90°,BC=2,点P是线段AB上的动点,若线段CD上存在点Q,使得异面直线PQ与AC成30°的角,则线段PA长的取值范围是( )
如图,在三棱锥A-BCD中,平面ABC⊥平面BCD,△BAC与△BCD均为等腰直角三角形,且∠BAC=∠BCD=90°,BC=2,点P是线段AB上的动点,若线段CD上存在点Q,使得异面直线PQ与AC成30°的角,则线段PA长的取值范围是( )| A. | (0,$\frac{\sqrt{2}}{2}$) | B. | (0,$\frac{\sqrt{6}}{3}$) | C. | ($\frac{\sqrt{2}}{2}$,$\sqrt{2}$) | D. | ($\frac{\sqrt{6}}{3}$,$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{{\sqrt{2}}}{2},1)$ | B. | $(0,\frac{{\sqrt{2}}}{2})$ | C. | $(\frac{{\sqrt{3}}}{2},1)$ | D. | $(0,\frac{{\sqrt{3}}}{2})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com