
分析 根据等比数列与正弦、余弦定理,利用基本不等式求出cosB的最小值,
得出此时A=B=C=$\frac{π}{3}$,从而求出$\frac{1}{tanA}$+$\frac{1}{tanC}$的值.
解答 解:△ABC中,sinA,ainB,sinC成等比数列,
∴sin2B=sinAsinC,
∴b2=ac;
∴cosB=$\frac{{a}^{2}{+c}^{2}{-b}^{2}}{2ac}$≥$\frac{2ac-ac}{2ac}$=$\frac{1}{2}$,
当且仅当a=c时取“=”;
∴cosB的最小值是$\frac{1}{2}$,且a=c;
∴A=C,
∴A=B=C=$\frac{π}{3}$,
∴$\frac{1}{tanA}$+$\frac{1}{tanC}$=$\frac{1}{\sqrt{3}}$+$\frac{1}{\sqrt{3}}$=$\frac{2\sqrt{3}}{3}$.
故答案为:$\frac{2\sqrt{3}}{3}$.
点评 本题考查了正弦、余弦定理及等比数列的性质与应用问题,也考查了基本不等式的应用问题,是综合题.


 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{25}$ | B. | $\frac{13}{125}$ | C. | $\frac{18}{125}$ | D. | $\frac{9}{125}$ |
查看答案和解析>>
科目:高中数学 来源:2017届湖南衡阳县四中高三9月月考数学(文)试卷(解析版) 题型:选择题
下列命题中正确的是( )
A.若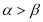 ,则
,则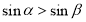 ;
;
B.命题:“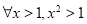 ”的否定是“
”的否定是“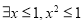 ”;
”;
C.直线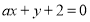 与
与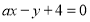 垂直的充要条件为
垂直的充要条件为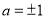 ;
;
D.“若 ,则
,则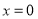 或
或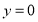 ”的逆否命题为“若
”的逆否命题为“若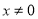 或
或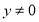 ,则
,则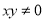 ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
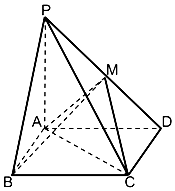 如图,在四棱锥P-ABCD,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD于点M.
如图,在四棱锥P-ABCD,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD于点M.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
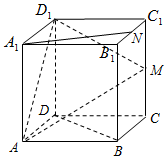 如图边长为2的正方体ABCD-A1B1C1D1中,M,N分别是CC1,B1C1的中点,
如图边长为2的正方体ABCD-A1B1C1D1中,M,N分别是CC1,B1C1的中点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{{\sqrt{2}}}{2},1)$ | B. | $(0,\frac{{\sqrt{2}}}{2})$ | C. | $(\frac{{\sqrt{3}}}{2},1)$ | D. | $(0,\frac{{\sqrt{3}}}{2})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com