
| m |
| n |
| 3 |
| m |
| n |
科目:高中数学 来源: 题型:
| πx |
| 2 |
| πx |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
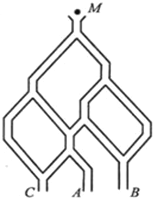 如图,一个小球从 M处投入,通过管道自上而下落A或B或C.已知小球从每个叉口落入左右两个管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到A,B,C,则分别设为l,2,3等奖.
如图,一个小球从 M处投入,通过管道自上而下落A或B或C.已知小球从每个叉口落入左右两个管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到A,B,C,则分别设为l,2,3等奖.查看答案和解析>>
科目:高中数学 来源: 题型:
| 数学 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
| 物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
| ? |
| y |
| |||||||
|
. |
| y |
. |
| x |
| ? |
| y |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com