
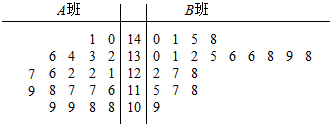
 为备战“全国高中数学联赛”,我市某高中拟成立两个“数学竞赛班”,经过学校预选,选出40名学生,编成A,B两个班,分别由两位教师担任教练进行培训;经过两个月的培训,参加了市里组织的数学竞赛初赛(只有经过初赛,取得相应名次,才能取得参加省统一组织的“全国高中数学联赛”复赛资格),这40名学生的初赛成绩的茎叶图如图:
为备战“全国高中数学联赛”,我市某高中拟成立两个“数学竞赛班”,经过学校预选,选出40名学生,编成A,B两个班,分别由两位教师担任教练进行培训;经过两个月的培训,参加了市里组织的数学竞赛初赛(只有经过初赛,取得相应名次,才能取得参加省统一组织的“全国高中数学联赛”复赛资格),这40名学生的初赛成绩的茎叶图如图:| A班 | B班 | 合计 | |
| 种子选手 | |||
| 非种子选手 | |||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)根据茎叶图可知A班数据的重心偏下,可得:故$\overline{{x}_{A}}$<$\overline{{x}_{B}}$;
(2)根据茎叶图求出列联表中各个数据,计算出临界值,可得结论;
(3)由(2)知:种子选手共13人,其中获市一等奖的人数为6人,由题意,X满足参数为13,6,3的超几何分布所以X的所有可能取值为0,1,2,3,求出相应的概率,可得答案.
解答 解:(1)茎叶图可知A班数据的重心偏下,故$\overline{{x}_{A}}$<$\overline{{x}_{B}}$;
(2)由茎叶图可知,“种子选手”共有13名,其中A班3人,B班10人,非种子选手27人,其中A班17人,B班10人,从而2×2联表如下:
| A班 | B班 | 合计 | |
| 种子选手 | 3 | 10 | 13 |
| 非种子选手 | 17 | 10 | 27 |
| 合计 | 20 | 20 | 40 |
| X | 0 | 1 | 2 | 3 |
| P | $\frac{35}{286}$ | $\frac{63}{143}$ | $\frac{105}{286}$ | $\frac{10}{143}$ |
点评 本题考查的知识点是独立性检验,茎叶图,古典概型,是统计和概率的综合应用,难度中档.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 5000辆汽车通过某一段公路时的时速频率分布直方图如图所示.问:
5000辆汽车通过某一段公路时的时速频率分布直方图如图所示.问:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=0.4x | B. | y=lgx+1 | C. | y=x${\;}^{\frac{3}{2}}$ | D. | y=1.125x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-2)2+(y+1)2=2 | B. | (x+2)2+(y-1)2=4 | C. | (x-2)2+(y+1)2=8 | D. | (x+2)2+(y-1)2=8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com