
【题目】石家庄市为鼓励居民节约用电,采用分段计费的方法计算电费,每月用电不超过100度时,按每度0.52元计算,每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.6元计算.
(1)设月用电x度时,应缴电费y元,写出y关于x的函数关系式;
(2)小明家第一季度缴纳电费情况如表:
月份 | 一月 | 二月 | 三月 | 合计 |
缴费金额 | 82元 | 64元 | 46.8元 | 192.8元 |
问小明家第一季度共用电多少度?
【答案】
(1)解:由题意:每月用电不超过100度时,按每度0.52元计算:
可得y=0.52x,(0≤x≤100);
每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.6元计算.
可得:y=52+(x﹣100)×0.6,(x>100);
故而可得y关于x的函数关系式为 ![]()
(2)解:由(1)可知,按每度0.52元计算的最高费用是52元;
一月:∵82>52,
∴0.6x﹣8=82,x=150,
二月:∵64>52,
∴0.6x﹣8=64,x=120.
三月:∵46.8<52,
∴0.52x=46.8,x=90.
∴共用150+120+90=360度.
答:小明家第一季度共用电360度
【解析】(1)根据题意,采用分段计费的方法计算电费,其为分段函数,利用分段函数的性质求解即可.(2)根据分函数的解析式,带值计算.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案科目:高中数学 来源: 题型:
【题目】设f(x)为定义R在的偶函数,当0≤x≤2时,y= ![]() ;当x>2时,y=f(x)的图象是顶点在p(3,4),且过点A(2,3)的抛物线的一部分.
;当x>2时,y=f(x)的图象是顶点在p(3,4),且过点A(2,3)的抛物线的一部分.
(1)求函数f(x)的解析式;
(2)在下面的直角坐标系中直接画出函数f(x)的图象,写出函数f(x)的单调区间(无需证明).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(4x+1)﹣x,g(x)=log2a+log2(2x﹣ ![]() )(a>0,x>1).
)(a>0,x>1).
(1)证明函数f(x)为偶函数;
(2)若函数f(x)﹣g(x)只有一个零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应国家“精准扶贫,产业扶贫”的战略,某市面向全市征召《扶贫政策》义务宣传志愿者,从年龄在![]() 的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示.
的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示.
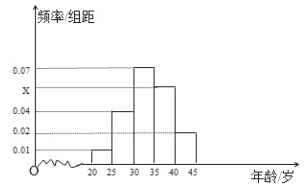
(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取10名参加中心广场的宣传活动,再从这10名志愿者中选取3名担任主要负责人.记这3名志愿者中“年龄低于35岁”的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数:R(x)=  ,其中x是仪器的月产量.(注:总收益=总成本+利润)
,其中x是仪器的月产量.(注:总收益=总成本+利润)
(1)将利润x表示为月产量x的函数;
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,函数g(x)=b﹣f(2﹣x),其中b∈R,若函数y=f(x)﹣g(x)恰有4个零点,则b的取值范围是( )
,函数g(x)=b﹣f(2﹣x),其中b∈R,若函数y=f(x)﹣g(x)恰有4个零点,则b的取值范围是( )
A.( ![]() ,+∞)
,+∞)
B.(﹣∞, ![]() )
)
C.(0, ![]() )
)
D.( ![]() ,2)
,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“杨辉三角”又称“贾宪三角”,是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算,而杨辉在公元1261年所著的《详解九章算法》一书中,记录了贾宪三角形数表,并称之为“开方作法本源”图.下列数表的构造思路就源于“杨辉三角”.该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg(ax﹣bx)(a>1>b>0).
(1)求f(x)的定义域;
(2)若f(x)在(1,+∞)上递增且恒取正值,求a,b满足的关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com