
【题目】甲、乙两人进行象棋比赛,采取五局三胜制(不考虑平局,先赢得三场的人为获胜者,比赛结束).根据前期的统计分析,得到甲在和乙的第一场比赛中,取胜的概率为0.5,受心理方面的影响,前一场比赛结果会对甲的下一场比赛产生影响,如果甲在某一场比赛中取胜,则下一场取胜率提高0.1,反之,降低0.1.则甲以3:1取得胜利的概率为( )
A.0.162B.0.18C.0.168D.0.174
 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,将曲线
中,将曲线![]() (
(![]() 为参数) 上任意一点
为参数) 上任意一点![]() 经过伸缩变换
经过伸缩变换![]() 后得到曲线
后得到曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,建立极坐标系,直线
轴的非负半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,
两点,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在区间
在区间![]() 单调递增,下述三个结论:①
单调递增,下述三个结论:①![]() 的取值范围是
的取值范围是![]() ;②
;②![]() 在
在![]() 存在零点;③
存在零点;③![]() 在
在![]() 至多有4个极值点.其中所有正确结论的编号是( )
至多有4个极值点.其中所有正确结论的编号是( )
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】生活中人们常用“通五经贯六艺”形容一个人才识技艺过人,这里的“六艺”其实源于中国周朝的贵族教育体系,具体包括“礼、乐、射、御、书、数”. 为弘扬中国传统文化,某校在周末学生业余兴趣活动中开展了“六艺”知识讲座,每艺安排一节,连排六节,则满足“数”必须排在前两节,“礼”和“乐”必须相邻安排的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的右准线为直线
的右准线为直线![]() ,左顶点为
,左顶点为![]() ,右焦点为
,右焦点为![]() . 已知斜率为2的直线
. 已知斜率为2的直线![]() 经过点
经过点![]() ,与椭圆
,与椭圆![]() 相交于
相交于![]() 两点,且
两点,且![]() 到直线
到直线![]() 的距离为
的距离为![]()
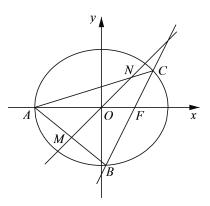
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若过![]() 的直线
的直线![]() 与直线
与直线![]() 分别相交于
分别相交于![]() 两点,且
两点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面
的底面![]() 为平行四边形,
为平行四边形,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
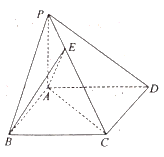
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)在侧棱![]() 上是否存在点E,使
上是否存在点E,使![]() 与底面
与底面![]() 所成的角为45°?若存在,求
所成的角为45°?若存在,求![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年新型冠状病毒疫情爆发,贵州省教育厅号召全体学生“停课不停学”.自
年新型冠状病毒疫情爆发,贵州省教育厅号召全体学生“停课不停学”.自![]() 月
月![]() 日起,高三年级学生通过收看“阳光校园·空中黔课”进行线上网络学习.为了检测线上网络学习效果,某中学随机抽取
日起,高三年级学生通过收看“阳光校园·空中黔课”进行线上网络学习.为了检测线上网络学习效果,某中学随机抽取![]() 名高三年级学生做“是否准时提交作业”的问卷调查,并组织了一场线上测试,调查发现有
名高三年级学生做“是否准时提交作业”的问卷调查,并组织了一场线上测试,调查发现有![]() 名学生每天准时提交作业,根据他们的线上测试成绩得频率分布直方图(如图
名学生每天准时提交作业,根据他们的线上测试成绩得频率分布直方图(如图![]() 所示);另外
所示);另外![]() 名学生偶尔没有准时提交作业,根据他们的线上测试成绩得茎叶图(如图
名学生偶尔没有准时提交作业,根据他们的线上测试成绩得茎叶图(如图![]() 所示,单位:分)
所示,单位:分)
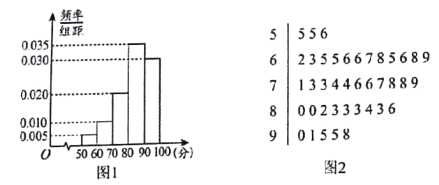
(1)成绩不低于![]() 分为
分为![]() 等,低于
等,低于![]() 分为非
分为非![]() 等.完成以下列联表,并判断是否有
等.完成以下列联表,并判断是否有![]() 以上的把握认为成绩取得
以上的把握认为成绩取得![]() 等与每天准时提交作业有关?
等与每天准时提交作业有关?
准时提交作业与成绩等次列联表 | 单位:人 | ||
A等 | 非A等 | 合计 | |
每天准时提交作业 | |||
偶尔没有准时提交作业 | |||
合计 | |||
(2)成绩低于![]() 分为不合格,从这
分为不合格,从这![]() 名学生里成绩不合格的学生中再抽取
名学生里成绩不合格的学生中再抽取![]() 人,其中每天准时提交作业的学生人数为
人,其中每天准时提交作业的学生人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
附: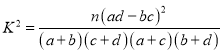
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com