
已知函数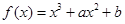 的图象上一点P(1,0),且在P点处的切线与直线
的图象上一点P(1,0),且在P点处的切线与直线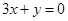 平行.
平行.
(1)求函数 的解析式;
的解析式;
(2)求函数 在区间[0,t](0<t<3)上的最大值和最小值;
在区间[0,t](0<t<3)上的最大值和最小值;
(3)在(1)的结论下,关于x的方程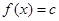 在区间[1,3]上恰有两个相异的实根,求实数c的取值范围
在区间[1,3]上恰有两个相异的实根,求实数c的取值范围
(1)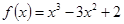 (2)答案见解析 (3)
(2)答案见解析 (3)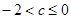
解析试题分析:(1)由
科目:高中数学
来源:
题型:解答题
某商场销售某种商品的经验表明,该商品每日的销售量
科目:高中数学
来源:
题型:填空题
若函数y=f(x)的图象与函数
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区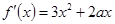 及曲线在
及曲线在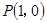 处的切线斜率为
处的切线斜率为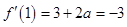 ,即可求得
,即可求得 ,又函数过
,又函数过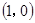 点,即可求的
点,即可求的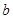 .
.
(2)由(1)易知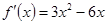 ,令
,令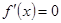 可得
可得 或
或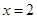 ,然后对
,然后对 进行分类讨论,确定函数
进行分类讨论,确定函数 在
在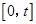 的单调性,即可求出函数
的单调性,即可求出函数 在
在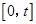
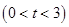 上的最大值和最小值;
上的最大值和最小值;
(3)构造函数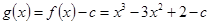 ,研究函数
,研究函数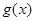 的单调性,列出该方程有两个相异的实根的不等式组,求出实数
的单调性,列出该方程有两个相异的实根的不等式组,求出实数 的取值范围.
的取值范围.
试题解析:(1)因为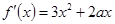 ,曲线在
,曲线在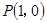 处的切线斜率为
处的切线斜率为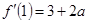 ,即
,即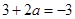 ,所以
,所以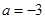 .
.
又函数过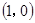 点,即
点,即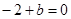 ,所以
,所以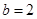 .
.
所以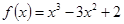 .
.
(2)由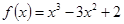 ,
,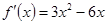 .
.
由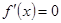 ,得
,得 或
或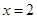 .
.
①当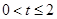 时,在区间
时,在区间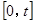 上
上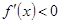 ,
, 在
在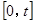 上是减函数,
上是减函数,
所以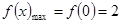 ,
,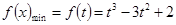 .
.
②当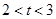 时,当
时,当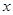 变化时,
变化时, 、
、 的变化情况见下表:
的变化情况见下表: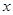
0 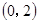
2 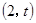
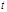


快乐口算系列答案
决胜百分百系列答案
小升初真题精选系列答案
基础天天练系列答案
夺冠训练归类模拟总复习系列答案
天府优学系列答案
小升初模拟冲刺卷系列答案
新考题大集结系列答案
中学英语听读导航系列答案
同步宝典1线超越系列答案
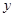 (单位:千克)与销售价格
(单位:千克)与销售价格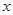 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式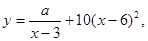 其中
其中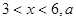 为常数。己知销售价格为5元/千克时,每日可售出该商品11千克.
为常数。己知销售价格为5元/千克时,每日可售出该商品11千克.
(1)求 的值;
的值;
(2)若该商品的成本为3元/千克,试确定销售价格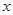 的值,使商场每日销售该商品所获得的利润最大.
的值,使商场每日销售该商品所获得的利润最大.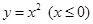 的图象关于直线x-y=0对称,则f(x)=
的图象关于直线x-y=0对称,则f(x)=
__________________________________.
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号