
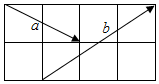
 如图,在2×4的方格纸中,若起点和终点均在格点的向量$\overrightarrow{a}$,$\overrightarrow{b}$,则向量$\overrightarrow{a}$+$\overrightarrow{b}$,$\overrightarrow{a}$-$\overrightarrow{b}$的夹角余弦值是-$\frac{4\sqrt{65}}{65}$.
如图,在2×4的方格纸中,若起点和终点均在格点的向量$\overrightarrow{a}$,$\overrightarrow{b}$,则向量$\overrightarrow{a}$+$\overrightarrow{b}$,$\overrightarrow{a}$-$\overrightarrow{b}$的夹角余弦值是-$\frac{4\sqrt{65}}{65}$. 分析 建立坐标系,求出向量的坐标,代入夹角公式计算.
解答 解:设每个小正方形的边长为1,建立如图所示的平面直角坐标系,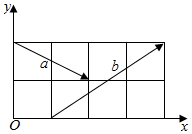
则$\overrightarrow{a}$=(2,-1),$\overrightarrow{b}$=(3,2).
∴$\overrightarrow{a}+\overrightarrow{b}$=(5,1),$\overrightarrow{a}-\overrightarrow{b}$=(-1,-3).
∴($\overrightarrow{a}+\overrightarrow{b}$)•($\overrightarrow{a}-\overrightarrow{b}$)=-5-3=-8.|$\overrightarrow{a}-\overrightarrow{b}$|=$\sqrt{10}$,|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{26}$.
∴向量$\overrightarrow{a}$+$\overrightarrow{b}$,$\overrightarrow{a}$-$\overrightarrow{b}$的夹角余弦值为$\frac{-8}{\sqrt{10}\sqrt{26}}$=-$\frac{4\sqrt{65}}{65}$.
故答案为:-$\frac{4\sqrt{65}}{65}$.
点评 本题考查了平面向量的数量积运算,属于中档题.


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:高中数学 来源: 题型:选择题
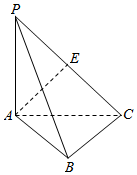 如图所示,三棱锥P-ABC中,PA⊥平面ABC,△ABC为正三角形,PA=AB,E是PC的中点,则异面直线AE和PB所成角的余弦值为( )
如图所示,三棱锥P-ABC中,PA⊥平面ABC,△ABC为正三角形,PA=AB,E是PC的中点,则异面直线AE和PB所成角的余弦值为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com