
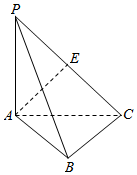
 如图所示,三棱锥P-ABC中,PA⊥平面ABC,△ABC为正三角形,PA=AB,E是PC的中点,则异面直线AE和PB所成角的余弦值为( )
如图所示,三棱锥P-ABC中,PA⊥平面ABC,△ABC为正三角形,PA=AB,E是PC的中点,则异面直线AE和PB所成角的余弦值为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
分析 取BC的中点F,连接EF,AF,得到∠AEF或其补角就是异面直线AE和PB所成角,由此能求出异面直线AE和PB所成角的余弦值.
解答 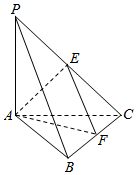 解:取BC的中点F,连接EF,AF
解:取BC的中点F,连接EF,AF
则EF∥PB,
∴∠AEF或其补角就是异面直线AE和PB所成角,
∵△ABC为正三角形,∴∠BAC=60°.
设PA=AB=2a,PA⊥平面ABC,
∴$AF=\sqrt{3}a,AE=\sqrt{2}a,EF=\sqrt{2}a$,
∴$cos∠AEF=\frac{{{{(\sqrt{2}a)}^2}+{{(\sqrt{2}a)}^2}-{{(\sqrt{3}a)}^2}}}{{2×\sqrt{2}a×\sqrt{2}a}}=\frac{1}{4}$.
∴异面直线AE和PB所成角的余弦值为$\frac{1}{4}$.
故选:B.
点评 本题考查异面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 34 | B. | 32 | C. | 30 | D. | 28 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | -$\frac{4}{3}$ | D. | -$\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,2x≠3 | B. | ?x>0,2x≠3 | C. | ?x≤0,2x=3 | D. | ?x≤0,2x≠3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
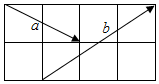 如图,在2×4的方格纸中,若起点和终点均在格点的向量$\overrightarrow{a}$,$\overrightarrow{b}$,则向量$\overrightarrow{a}$+$\overrightarrow{b}$,$\overrightarrow{a}$-$\overrightarrow{b}$的夹角余弦值是-$\frac{4\sqrt{65}}{65}$.
如图,在2×4的方格纸中,若起点和终点均在格点的向量$\overrightarrow{a}$,$\overrightarrow{b}$,则向量$\overrightarrow{a}$+$\overrightarrow{b}$,$\overrightarrow{a}$-$\overrightarrow{b}$的夹角余弦值是-$\frac{4\sqrt{65}}{65}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com