练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．已知数列{an}是正项等比数列，若a2a9a16=64，则log2a1+log2a2+…+log2a17=（　　）
    A．34B．32C．30D．28

    分析 由已知结合等比数列的性质求得a9=4．再由对数的运算性质可得log2a1+log2a2+…+log2a17=$lo{g}_{2}{{a}_{9}}^{17}$，代入a9得答案．

    解答 解：在正项等比数列{an}中，
    由a2a9a16=64，得${{a}_{9}}^{3}=64$，即a9=4．
    ∴log2a1+log2a2+…+log2a17=$lo{g}_{2}（{a}_{1}{a}_{2}…{a}_{17}）=lo{g}_{2}{{a}_{9}}^{17}$=$lo{g}_{2}{4}^{17}=34$．
    故选：A．

    点评 本题考查等比数列的通项公式，考查了等比数列的性质，考查对数的运算性质，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    13．已知正项数列{an}满足2a1+3a2+a3=1，则$\frac{1}{{{a_1}+{a_2}}}$与$\frac{1}{{{a_2}+{a_3}}}$的等差中项最小为$\frac{{3+2\sqrt{2}}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知各项均为正数的数列{an}的前n项和为Sn，且an2+2an=4Sn．
    （1）求Sn；
    （2）设bn=（$\sqrt{n+1}$+$\sqrt{n}$）•$\sqrt{S_n}$，求数列{${\frac{1}{b_n}}\right.$}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．经销商经销某种产品，在一个销售周期内，每售出1件产品获得利润500元，未售出的产品每件亏损100元．根据过去的市场记录，得到了60个销售周期的市场需求量的频数分布表：
    需求量[100，110）[110，120）[120，130）[130，140）[140，150]
    频数61218159
    经销商为了下一个销售周期购进了130件产品，以X（100≤X≤150）表示下一个销售周期内的市场需求量，Y表示下一个销售周期内的经销产品的利润．
    （1）画出市场需求量的频率分布直方图，并以各组的区间中点值代表该组的各个需求量，估计一个销售周期内的市场需求量的平均数；
    （2）根据市场需求量的频数分布表提供的数据，估计下一个销售周期内的经销产品利润Y不少于53000元的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．设点P（x，y）在不等式组$\left\{\begin{array}{l}{x≥0，}&{\;}\\{2x-y≤0，}&{\;}\\{x+y-3≤0}&{\;}\end{array}\right.$表示的平面区域上，则z=$\sqrt{{x}^{2}+{y}^{2}-2x+1}$的最小值为（　　）
    A．1B．$\frac{\sqrt{5}}{5}$C．2D．$\frac{2\sqrt{5}}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．太极图是以黑白两个鱼形纹组成的圆形图案，俗称阴阳鱼．太级图形展现了一种互相转化，相对统一的形式美、和谐美．现在定义：能够将圆O的周长和面积同时分为相等的两部分的函数称为圆O的“太极函数”，给出下列命题：
    p1：对于任意一个圆O，其对应的“太极函数”不唯一；
    p2：f（x）=ex+e-x可能是某个圆的一个“太极函数”；
    p3：圆O：（x-1）2+y2=36的一个“太极函数”为f（x）=-ln$\frac{5+x}{7-x}$；
    p4：“太极函数”的图象一定是中心对称图形．
    其中正确的命题是（　　）
    A．p1，p2B．p1，p3C．p2，p3D．p3，p4

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$是夹角为$\frac{π}{3}$的两个单位向量，$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$，$\overrightarrow{b}$=$\overrightarrow{{e}_{1}}$-k$\overrightarrow{{e}_{2}}$，若$\overrightarrow{a}$•$\overrightarrow{b}$=0，则k的值为-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知当x∈（1，2）时，不等式x2+x+m＜0恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

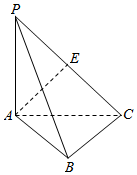    9．如图所示，三棱锥P-ABC中，PA⊥平面ABC，△ABC为正三角形，PA=AB，E是PC的中点，则异面直线AE和PB所成角的余弦值为（　　）
    A．$\frac{1}{6}$B．$\frac{1}{4}$C．$\frac{1}{3}$D．$\frac{1}{2}$

    查看答案和解析>>

    同步练习册答案