
 经销商经销某种产品,在一个销售周期内,每售出1件产品获得利润500元,未售出的产品每件亏损100元.根据过去的市场记录,得到了60个销售周期的市场需求量的频数分布表:
经销商经销某种产品,在一个销售周期内,每售出1件产品获得利润500元,未售出的产品每件亏损100元.根据过去的市场记录,得到了60个销售周期的市场需求量的频数分布表:| 需求量 | [100,110) | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 6 | 12 | 18 | 15 | 9 |
分析 (1)根据频数分布表绘制频率分布直方图,求出一个销售周期内的市场需求量的平均数;
(2)由题意先分段写出,当X∈[100,130)及X∈[130,150)时,和利润值,最后利用分段函数的形式进行综合即可.利润T不少于53000元,解得:110≤X≤150,.再由直方图知需求量X∈[100,110]的频率为0.1,即可求得下一个销售季度的利润Y不少于53000元的概率.
解答 解:(1)频率分布直方图如下图所示: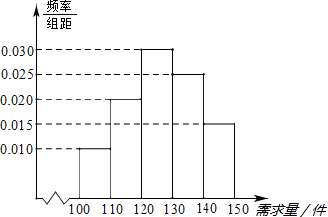
∵$\frac{105×6+115×12+125×18+135×15+145×9}{60}$=126.5,
∴估计一个销量周期内的市场需求量的平均数为126.5;
(2)当X∈[100,130)时,Y=500X-100(130-X)=600X-13000,
当X∈[130,150]时,Y=500×130=65000,
∴Y=$\left\{\begin{array}{l}{600X-13000,}&{X∈[100,130)}\\{65000,}&{X∈[130,150]}\end{array}\right.$,
令Y≥53000,解得110≤X≤150,
∵100≤X≤110时,一个销量周期内的经销产品的需求量的概率为$\frac{6}{60}$=0.1,
下一个销量周期内的经销产品的利润Y不少于53000元的概率为1-0.1=0.9.
点评 本题考查根据频数分布表绘制样本频率分布直方图以及用样本的频率分布估计总体分布及识图的能力,求解的重点是对题设条件及直方图的理解,了解直方图中每个小矩形的面积的意义,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,4] | B. | (0,52] | C. | [52,+∞) | D. | [36,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 一个圆锥被过顶点的平面截去了较小的一部分几何体,余下的几何体的三视图如图,则余下部分的几何体的体积为( )
一个圆锥被过顶点的平面截去了较小的一部分几何体,余下的几何体的三视图如图,则余下部分的几何体的体积为( )| A. | $\frac{\sqrt{2}}{3}$+$\frac{\sqrt{2}}{2}$π | B. | $\sqrt{2}$+$\frac{\sqrt{2}}{2}$π | C. | $\sqrt{2}$+$\frac{3\sqrt{2}}{2}$π | D. | 2$\sqrt{2}$+3$\sqrt{2}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1<x≤2} | B. | {x|1<x<2} | C. | {x|x>2} | D. | {x|x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 34 | B. | 32 | C. | 30 | D. | 28 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 31 | B. | 30 | C. | 28 | D. | 26 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com