
分析 (1)当n≥2时,2(Sn-Sn-1)=(n+1)($\frac{1}{S_1}$+$\frac{1}{S_2}$+…+$\frac{1}{S_n}$),令n=2,则2a2=3$(1+\frac{1}{1+{a}_{2}})$,解得a2=2.猜想an=n,可得Sn=$\frac{n(n+1)}{2}$,利用数学归纳法证明即可得出.
(2)要证明:4anan≤${a_{n+2}}^{{a_{n+2}}-2}$,(n≥2),即证明:4nn≤(n+2)n,即证明$(1+\frac{2}{n})^{n}$≥4,利用二项式定理展开:$(1+\frac{2}{n})^{n}$=${∁}_{n}^{0}$+${∁}_{n}^{1}•\frac{2}{n}$+${∁}_{n}^{2}•(\frac{2}{n})^{2}$+…,即可证明.
解答 (1)解:当n≥2时,2(Sn-Sn-1)=(n+1)($\frac{1}{S_1}$+$\frac{1}{S_2}$+…+$\frac{1}{S_n}$),
令n=2,则2a2=3$(1+\frac{1}{1+{a}_{2}})$,化为:$2{a}_{2}^{2}$-a2-6=0,a2>0,解得a2=2.
猜想an=n,
下面利用数学归纳法给出证明:
①n=1,2时成立.
②假设n=k时成立,则Sk=$\frac{k(k+1)}{2}$,可得$\frac{1}{{S}_{k}}$=$\frac{2}{k(k+1)}$=2$(\frac{1}{k}-\frac{1}{k+1})$,
∴$\frac{1}{S_1}$+$\frac{1}{S_2}$+…+$\frac{1}{{S}_{k+1}}$=2$[(1-\frac{1}{2})$+$(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{k+1}-\frac{1}{k+2})]$=2$(1-\frac{1}{k+2})$=$\frac{2(k+1)}{k+2}$,
当n≥2时,2(Sk+1-Sk)=(k+2)($\frac{1}{S_1}$+$\frac{1}{S_2}$+…+$\frac{1}{{S}_{k+1}}$).
∴2ak+1=(k+2)×$\frac{2(k+1)}{k+2}$,
∴ak+1=k+1,
因此n=k+1时也成立.
综上可得:?n∈N*,an=n成立.
(2)证明:要证明:4anan≤${a_{n+2}}^{{a_{n+2}}-2}$,(n≥2),即证明:4nn≤(n+2)n,
即证明$(1+\frac{2}{n})^{n}$≥4,
利用二项式定理展开:$(1+\frac{2}{n})^{n}$=${∁}_{n}^{0}$+${∁}_{n}^{1}•\frac{2}{n}$+${∁}_{n}^{2}•(\frac{2}{n})^{2}$+…≥1+2+$\frac{2(n-1)}{n}$≥4,(n≥2).
∴$(1+\frac{2}{n})^{n}$≥4成立,
∴4anan≤${a_{n+2}}^{{a_{n+2}}-2}$,(n≥2).
点评 本题考查了递推关系、二项式定理、猜想归纳验证方法,考查了分析问题与解决问题的能力、推理能力与计算能力,属于难题.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | -$\frac{4}{3}$ | D. | -$\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
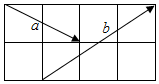 如图,在2×4的方格纸中,若起点和终点均在格点的向量$\overrightarrow{a}$,$\overrightarrow{b}$,则向量$\overrightarrow{a}$+$\overrightarrow{b}$,$\overrightarrow{a}$-$\overrightarrow{b}$的夹角余弦值是-$\frac{4\sqrt{65}}{65}$.
如图,在2×4的方格纸中,若起点和终点均在格点的向量$\overrightarrow{a}$,$\overrightarrow{b}$,则向量$\overrightarrow{a}$+$\overrightarrow{b}$,$\overrightarrow{a}$-$\overrightarrow{b}$的夹角余弦值是-$\frac{4\sqrt{65}}{65}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com