
德国著名数学家狄利克雷在数学领域成就显著,以其命名的函数f(x)=被称为狄利克雷函数,其中R为实数集,Q为有理数集,则关于函数f(x)有如下四个命题:
①f(f(x))=0;
②函数f(x)是偶函数;
③f(x)是周期函数;
④存在三个点A(x1,f(x1)),B(x2,f(x2)),C(x3,f(x3)),使得△ABC为等边三角形;
⑤存在三个点A(x1,f(x1)),B(x2,f(x2)),C(x3,f(x3)),使得△ABC为直角三角形.
其中真命题的个数是( )
A.1 B.2 C.3 D.4
D
【解析】
试题分析:①∵当x为有理数时,f(x)=1;当x为无理数时,f(x)=0
∴当x为有理数时,f(f(x))=f(1)=1;当x为无理数时,f(f(x))=f(0)=1
即不管x是有理数还是无理数,均有f(f(x))=1,故①不正确;
②∵有理数的相反数还是有理数,无理数的相反数还是无理数,
∴对任意x∈R,都有f(-x)=-f(x),故②正确;
③任取非零有理数T,若x是有理数,则x+T也是有理数;
若x是无理数,则x+T也是无理数
∴根据函数的表达式,f(x+T)=f(x)对x∈R恒成立,故③正确;
④取x1=-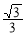 ,x2=0,x3=
,x2=0,x3=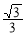 ,可得f(x1)=0,f(x2)=1,f(x3)=0
,可得f(x1)=0,f(x2)=1,f(x3)=0
∴A(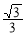 ,0),B(0,1),C(-
,0),B(0,1),C(-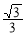 ,0),恰好△ABC为等边三角形,故④正确.
,0),恰好△ABC为等边三角形,故④正确.
⑤取x1=-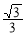 ,x2=0,x3=
,x2=0,x3=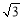 ,可得f(x1)=0,f(x2)=1,f(x3)=0
,可得f(x1)=0,f(x2)=1,f(x3)=0
∴A(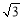 ,0),B(0,1),C(-
,0),B(0,1),C(-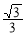 ,0),恰好△ABC为直角三角形,故⑤正确.
,0),恰好△ABC为直角三角形,故⑤正确.
考点:分段函数的综合应用


科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试理科数学试卷(解析版) 题型:填空题
定义一:对于一个函数f(x)(x∈D),若存在两条距离为d的直线y=kx+m1和y=kx+m2,使得在x∈D时,kx+m1≤f(x)≤kx+m2 恒成立,则称函数f(x)在D内有一个宽度为d的.
定义二:若一个函数f(x),对于任意给定的正数?,都存在一个实数x0,使得函数f(x)在[x0,+∞)内有一个宽度为?的,则称f(x)在正无穷处有.下列函数:
①f(x)=lgx,②f(x)=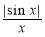 ,③f(x)=-
,③f(x)=-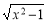 ,④f(x)=
,④f(x)=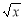 ,⑤f(x)=2x,⑥f(x)=3x-
,⑤f(x)=2x,⑥f(x)=3x-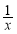
其中在正无穷处有的函数的序号是___________.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试理科数学试卷(解析版) 题型:选择题
设f(x)=4sinxsin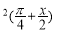 +cos2x,|f(x)-m|<3对?x∈(0,π)恒成立,则实数m的范围是( )
+cos2x,|f(x)-m|<3对?x∈(0,π)恒成立,则实数m的范围是( )
A.[0,4] B.(0,4] C.[0,4) D.(0,4)
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试文科数学试卷(解析版) 题型:解答题
数列{an}的前n项和为Pn,若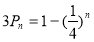 (n∈N*),数列{bn}满足2bn+1=bn+bn+2(n∈N*),且b3=7,b8=22.
(n∈N*),数列{bn}满足2bn+1=bn+bn+2(n∈N*),且b3=7,b8=22.
(1)求数列{an}和{bn}的通项公式an和bn;
(2)设数列cn=anbn,求{cn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试文科数学试卷(解析版) 题型:选择题
若(1+2ai)i=1-bi,其中a,b∈R,i是虚数单位,则|a+bi|=( )
A. +i B.
+i B.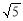 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考文科数学试卷(解析版) 题型:选择题
若p:x2﹣4x+3>0;q:x2<1,则p是q的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com