
【题目】如图,在直角坐标系![]() 中,椭圆
中,椭圆![]() 的上焦点为
的上焦点为![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点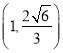 .
.
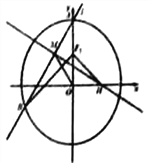
(1)求椭圆![]() 的方程.
的方程.
(2)设过椭圆![]() 的上顶点
的上顶点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)直线
;(2)直线![]() 的方程为
的方程为![]() .
.
【解析】试题分析:(1)根据椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点 ,结合性质
,结合性质![]() ,列出关于
,列出关于![]() 、
、![]() 、
、![]() 的方程组,求出
的方程组,求出![]() 、
、![]() 、
、![]() ,即可求得椭圆
,即可求得椭圆![]() 的标准方程;(2)设直线
的标准方程;(2)设直线![]() 的方程为
的方程为![]() ,由
,由 ,求得
,求得![]() 点坐标,求得
点坐标,求得![]() 点坐标,根据向量数量积的坐标运算列方程求得
点坐标,根据向量数量积的坐标运算列方程求得![]() ,即可求得直线
,即可求得直线![]() 的方程.
的方程.
试题解析:(1)因为椭圆的离心率为![]() ,所以
,所以![]()
即可得![]() ,所以椭圆
,所以椭圆![]() 的方程为
的方程为 ,
,
把点 代入
代入![]() 中,
中,
解得![]()
所以椭圆方程为![]()
(2)设直线![]() 的斜率为
的斜率为![]() ,
,
则直线![]() 的方程为
的方程为![]()
由
设由(1)知![]() ,设
,设![]() ,
,
则有![]()
所以![]() 所以
所以
因为![]() ,所以
,所以![]() 在线段
在线段![]() 的中垂线上.
的中垂线上.
所以![]() ,又
,又![]() ,
,
所以![]() ,即
,即![]() ,
,
设![]() ,又直线
,又直线![]() 垂直
垂直![]()
∴
∴![]() ,即
,即
又![]() ∴
∴ ,
, ![]()
又![]() ∴
∴![]()
![]()
所以直线![]() 的方程为
的方程为![]() .
.
【方法点晴】本题主要考查待定系数求椭圆方程以及直线与椭圆的位置关系和数量积公式,属于难题.用待定系数法求椭圆方程的一般步骤;①作判断:根据条件判断椭圆的焦点在![]() 轴上,还是在
轴上,还是在![]() 轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程
轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程![]() 或
或![]()
![]() ;③找关系:根据已知条件,建立关于
;③找关系:根据已知条件,建立关于![]() 、
、![]() 、
、![]() 的方程组;④得方程:解方程组,将解代入所设方程,即为所求.
的方程组;④得方程:解方程组,将解代入所设方程,即为所求.


科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() 是棱PD的中点,且
是棱PD的中点,且![]() ,
, ![]() .
.
(I)求证: ![]() ; (Ⅱ)求二面角
; (Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)若![]() 是
是![]() 上一点,且直线
上一点,且直线![]() 与平面
与平面![]() 成角的正弦值为
成角的正弦值为![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】4月23日是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查,下面是根据调查结果绘制的学生日均课外阅读时间(单位:min)的频率分布直方图,若将日均课外阅读时间不低于60 min的学生称为“书虫”,低于60 min的学生称为“懒虫”,

(1)求x的值并估计全校3 000名学生中“书虫”大概有多少名学生?(将频率视为概率)
(2)根据已知条件完成下面2×2的列联表,并判断能否在犯错误的概率不超过0.01的前提下认为“书虫”与性别有关:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年9月3日,抗战胜利71周年纪念活动在北京隆重举行,受到全国人民的瞩目.纪念活动包括举行纪念大会、阅兵式、拥待会和文艺晚会等,据统计,抗战老兵由于身体原因,参加纪念大会、阅兵式、招待会这个环节(可参加多个,也可都不参加)的情况及其概率如下表所示:

(Ⅰ)若m=2n,则从这60名抗战老兵中按照参加纪念活动的环节数分层抽取6人进行座谈,求从参加纪念活动环节数为1的抗战老兵中抽取的人数;
(Ⅱ)某医疗部门决定从(Ⅰ)中抽取的6名抗战老兵中随机抽取2名进行体检,求这2名抗战老兵中至少有1人参加纪念活动的环节数为3的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆x2+![]() =1(0<b<1)的左焦点为F,左、右顶点分别为A、C,上顶点为B,过F、B、C三点作圆P,其中圆心P的坐标为(m,n).
=1(0<b<1)的左焦点为F,左、右顶点分别为A、C,上顶点为B,过F、B、C三点作圆P,其中圆心P的坐标为(m,n).
(1)若FC是圆P的直径,求椭圆的离心率;
(2)若圆P的圆心在直线x+y=0上,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经统计,某校学生上学路程所需要时间全部介于![]() 与
与![]() 之间(单位:分钟).现从在校学生中随机抽取
之间(单位:分钟).现从在校学生中随机抽取![]() 人,按上学所学时间分组如下:第
人,按上学所学时间分组如下:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得打如图所示的频率分布直方图.
,得打如图所示的频率分布直方图.
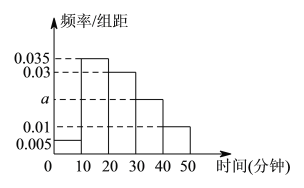
(Ⅰ)根据图中数据求![]() 的值.
的值.
(Ⅱ)若从第![]() ,
,![]() ,
,![]() 组中用分成抽样的方法抽取
组中用分成抽样的方法抽取![]() 人参与交通安全问卷调查,应从这三组中各抽取几人?
人参与交通安全问卷调查,应从这三组中各抽取几人?
(Ⅲ)在(Ⅱ)的条件下,若从这![]() 人中随机抽取
人中随机抽取![]() 人参加交通安全宣传活动,求第
人参加交通安全宣传活动,求第![]() 组至少有
组至少有![]() 人被抽中的概率.
人被抽中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com