练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．已知函数f（x）=ax3-3x的图象过点（-1，2），则a=1．

    分析 根据函数图象和点的坐标之间的关系进行求解．

    解答 解：∵函数f（x）=ax3-3x的图象过点（-1，2），
    ∴f（-1）=-a+3=2，
    解得a=1，
    故答案为：1

    点评 本题主要考查点的坐标与函数之间的关系，比较基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    18．已知A、B、C分别为△ABC的三边a、b、c所对的角，△ABC的面积为S，且$\sqrt{3}$$\overrightarrow{CA}$•$\overrightarrow{CB}$=2S．
    （Ⅰ）求角C的大小；
    （Ⅱ）若c=$\sqrt{6}$，求△ABC周长的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．以下四个数是数列{n（n+2）}的项的是 （　　）
    A．98B．99C．100D．101

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．设ξ～B（18，p），又E（ξ）=9，则p的值为（　　）
    A．$\frac{1}{2}$B．$\frac{1}{3}$C．$\frac{1}{4}$D．$\frac{2}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．应试教育下的高三学生身体素质堪忧，教育部门对某市100名高三学生的课外体育锻炼时间进行调查．他们的课外体育锻炼时间及相应的频数如下表：
    运动时间
    （单位：小时）    		$[0，\frac{1}{6}）$$[\frac{1}{6}，\frac{1}{3}）$$[\frac{1}{3}，\frac{1}{2}）$$[\frac{1}{2}，\frac{2}{3}）$$[\frac{2}{3}，\frac{5}{6}）$$[\frac{5}{6}，1）$
    总人数10182225205
    将学生日均课外体育运动时间在$[\frac{2}{3}，1）$上的学生评价为“课外体育达标”．
    （1）根据已知条件完成下面的2×2列联表：
    课外体育不达标课外体育达标合计
    男
    女1055
    合计
    （2）根据列联表的数据，若按95%的可靠性要求，能否认为“课外体育达标”与性别有关？
    附：${Χ^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．
    参考数据当Χ2≤2.706时，无充分证据判定变量A，B有关联，可以认为两变量无关联；
    当Χ2＞2.706时，有90%的把握判定变量A，B有关联；
    当Χ2＞3.841时，有95%的把握判定变量A，B有关联；
    当Χ2＞6.635时，有99%的把握判定变量A，B有关联．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．一个样本a，3，5，7的平均数是b，且a、b是方程x2-5x+4=0的两根，则这个样本的方差是5．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．某次数学测试中，小明完成前5道题所花的时间（单位：分钟）分别为4，5，6，x，y．已知这组数据的平均数为5，方差为$\frac{4}{5}$，则|x-y|的值为（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

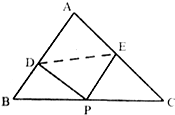    17．已知△ABC中，角A，B，C所对的边分别为a，b，c，若sin2 A+sin2 B=sin2C+sin AsinB，ccosB=b（1-cosC）．
    （1）判断△ABC的形状；
    （2）在△ABC的边AB，AC上分别取D，E两点，使沿线段DE折叠三角形时，顶点A正好落在边BC上的P点处，设∠BDP=θ，当AD最小时，求$\frac{{|{{A}D}|}}{{|{{A}{B}}|}}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知$\vec a=（4，2）$，$\vec b=（2，y）$，若$\vec a∥\vec b$，则y=（　　）
    A．1B．-1C．4D．-4

    查看答案和解析>>

    同步练习册答案