
| 运动时间 (单位:小时) | $[0,\frac{1}{6})$ | $[\frac{1}{6},\frac{1}{3})$ | $[\frac{1}{3},\frac{1}{2})$ | $[\frac{1}{2},\frac{2}{3})$ | $[\frac{2}{3},\frac{5}{6})$ | $[\frac{5}{6},1)$ |
| 总人数 | 10 | 18 | 22 | 25 | 20 | 5 |
| 课外体育不达标 | 课外体育达标 | 合计 | |
| 男 | |||
| 女 | 10 | 55 | |
| 合计 |
| 参考数据 | 当Χ2≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
| 当Χ2>2.706时,有90%的把握判定变量A,B有关联; | |
| 当Χ2>3.841时,有95%的把握判定变量A,B有关联; | |
| 当Χ2>6.635时,有99%的把握判定变量A,B有关联. |
分析 (1)由所给频数表知,在抽取的100人中,“课外体育达标”的学生有25人,从而可得2×2列联表;
(2)根据公式计算相关指数Χ2的观测值,比较临界值的大小,可判断按95%的可靠性要求,能否认为“课外体育达标”与性别有关.
解答 解:(1)由所给频数表知,在抽取的100人中,“课外体育达标”的学生有25人,从而2×2列联表如下:
| 课外体育不达标 | 课外体育达标 | 合计 | |
| 男 | 30 | 15 | 45 |
| 女 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
点评 本题考查了列联表及利用列联表进行独立性检验的思想方法,熟练掌握独立性检验的思想方法是解题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y平均增加1.5个单位 | B. | y平均减少1.5个单位 | ||
| C. | y平均增加2个单位 | D. | y平均减少2个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 方案一的平均损失比方案二的平均损失大 | |
| B. | 方案二的平均损失比方案一的平均损失大 | |
| C. | 方案一的平均损失与方案二的平均损失一样大 | |
| D. | 方案一的平均损失与方案二的平均损失无法计算 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,4) | B. | (-2,4) | C. | (-4,2) | D. | (-4,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
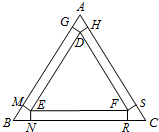 如图:在边长为6米的等边△ABC钢板内,作一个△DEF,使得△DEF的三边到△ABC所对应的三边之间的距离均x(0<x<$\frac{2}{3}$$\sqrt{3}$)米,过点D分别向AB,AC边作垂线,垂足依次为G,H;过点E分别向AB,BC边作垂线,垂足依次为M,N;过点F分别向BC,AC边作垂线,垂足依次为R,S.接着在△ABC的三个内角处,分别沿DG,DH、EM,EN、FR,FS进行切割,割去的三个全等的小四边形分别为AGDH、BMEN、CRFS.然后把矩形GDEM、NEFR、SFDH分别沿DE、EF、FD向上垂直翻折,并对翻折后的钢板进行无缝焊接(注:切割和无缝焊接过程中的损耗和费用忽略不计),从而构成一个无盖的正三棱柱蓄水池.
如图:在边长为6米的等边△ABC钢板内,作一个△DEF,使得△DEF的三边到△ABC所对应的三边之间的距离均x(0<x<$\frac{2}{3}$$\sqrt{3}$)米,过点D分别向AB,AC边作垂线,垂足依次为G,H;过点E分别向AB,BC边作垂线,垂足依次为M,N;过点F分别向BC,AC边作垂线,垂足依次为R,S.接着在△ABC的三个内角处,分别沿DG,DH、EM,EN、FR,FS进行切割,割去的三个全等的小四边形分别为AGDH、BMEN、CRFS.然后把矩形GDEM、NEFR、SFDH分别沿DE、EF、FD向上垂直翻折,并对翻折后的钢板进行无缝焊接(注:切割和无缝焊接过程中的损耗和费用忽略不计),从而构成一个无盖的正三棱柱蓄水池.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com