
 ��ͼ���ڱ߳�Ϊ6�ĵȱߡ�ABC�ְ��ڣ���һ����DEF��ʹ�á�DEF�����ߵ���ABC����Ӧ������֮��ľ����x��0��x��$\frac{2}{3}$$\sqrt{3}$���ף�����D�ֱ���AB��AC�������ߣ���������ΪG��H������E�ֱ���AB��BC�������ߣ���������ΪM��N������F�ֱ���BC��AC�������ߣ���������ΪR��S�������ڡ�ABC�������ڽǴ����ֱ���DG��DH��EM��EN��FR��FS�����и��ȥ������ȫ�ȵ�С�ı��ηֱ�ΪAGDH��BMEN��CRFS��Ȼ��Ѿ���GDEM��NEFR��SFDH�ֱ���DE��EF��FD���ϴ�ֱ���ۣ����Է��ۺ�ĸְ�����캸�ӣ�ע���и���캸�ӹ����е���ĺͷ��ú��Բ��ƣ����Ӷ�����һ���ǵ�����������ˮ�أ�
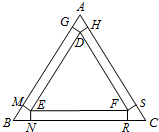
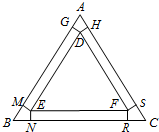
��ͼ���ڱ߳�Ϊ6�ĵȱߡ�ABC�ְ��ڣ���һ����DEF��ʹ�á�DEF�����ߵ���ABC����Ӧ������֮��ľ����x��0��x��$\frac{2}{3}$$\sqrt{3}$���ף�����D�ֱ���AB��AC�������ߣ���������ΪG��H������E�ֱ���AB��BC�������ߣ���������ΪM��N������F�ֱ���BC��AC�������ߣ���������ΪR��S�������ڡ�ABC�������ڽǴ����ֱ���DG��DH��EM��EN��FR��FS�����и��ȥ������ȫ�ȵ�С�ı��ηֱ�ΪAGDH��BMEN��CRFS��Ȼ��Ѿ���GDEM��NEFR��SFDH�ֱ���DE��EF��FD���ϴ�ֱ���ۣ����Է��ۺ�ĸְ�����캸�ӣ�ע���и���캸�ӹ����е���ĺͷ��ú��Բ��ƣ����Ӷ�����һ���ǵ�����������ˮ�أ����� ��1������BE�����EN������dz�������ˮ�ص������Ϊy����Ԫ����д��y�ı���ʽ��Ȼ�������Сֵ����2��д���dz�������ˮ�ص���������ù�ʽ�ĵ������жϺ����ĵ����������ֵ���ɣ�
���  ����С������16�֣�
����С������16�֣�
�⣺��1������BE���������֪����RT��BEN�У�
��EN=x���ף�����EBN=30��
��$tan{30^0}=\frac{EN}{BN}$����$BN=\sqrt{3}x���ף�$������2�֣�
������DEF�ı߳�Ϊ$6-2\sqrt{3}x���ף�$������3�֣�
������dz�������ˮ�ص������Ϊy����Ԫ����
��$y=[\frac{{\sqrt{3}}}{4}{��6-2\sqrt{3}x��^2}+3��6-2\sqrt{3}x��•x]•a$��$0��x��\frac{{2\sqrt{3}}}{3}$������5�֣�
=[$-3\sqrt{3}{x^2}+9\sqrt{3}$]•a
��$x=\frac{{2\sqrt{3}}}{3}��m��$ʱ��${y_{min}}=5\sqrt{3}a$����Ԫ��
�����dz�������ˮ������۵���СֵΪ$5\sqrt{3}a$����Ԫ������8�֣�
��2���������֪�����dz�������ˮ�ص����Ϊ��
$V=\frac{{\sqrt{3}}}{4}{��{6-2\sqrt{3}x}��^2}•x=\sqrt{3}��{3{x^3}-6\sqrt{3}{x^2}+9x}��$��$0��x��\frac{{2\sqrt{3}}}{3}$��������10�֣�
��V'=$\sqrt{3}��{9{x^2}-12\sqrt{3}x+9}��=3\sqrt{3}��{\sqrt{3}x-3}����{\sqrt{3}x-1}��$��
��V'=0������֮��$x=\frac{{\sqrt{3}}}{3}��x=\sqrt{3}∉��{0��\frac{{2\sqrt{3}}}{3}}]$������12�֣�
��$x�ʣ�{0��\frac{{\sqrt{3}}}{3}}]$ʱ��V'��0��������V��x����$x�ʣ�{0��\frac{{\sqrt{3}}}{3}}]$Ϊ��������������
��$x��[{\frac{{\sqrt{3}}}{3}��\frac{{2\sqrt{3}}}{3}}]$ʱ��V'��0��������V��x����$x��[{\frac{{\sqrt{3}}}{3}��\frac{{2\sqrt{3}}}{3}}]$Ϊ�����ݼ�������
��$x=\frac{{\sqrt{3}}}{3}���ף�$ʱ��${V_{max}}=4��{��^3}��$������15�֣�
�����dz�������ˮ�ص����V�����ֵΪ4��m3���� ����16�֣�
���� ���⿼�麯���뷽�̵�Ӧ�ã���������ֵ�������ĵ����뺯���ĵ����Ե�Ӧ�ã�������������������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �˶�ʱ�� ����λ��Сʱ�� | $[0��\frac{1}{6}��$ | $[\frac{1}{6}��\frac{1}{3}��$ | $[\frac{1}{3}��\frac{1}{2}��$ | $[\frac{1}{2}��\frac{2}{3}��$ | $[\frac{2}{3}��\frac{5}{6}��$ | $[\frac{5}{6}��1��$ |
| ������ | 10 | 18 | 22 | 25 | 20 | 5 |
| ������������� | ����������� | �ϼ� | |
| �� | |||
| Ů | 10 | 55 | |
| �ϼ� |
| �ο����� | ����2��2.706ʱ�����֤���ж�����A��B�й�����������Ϊ������������ |
| ����2��2.706ʱ����90%�İ����ж�����A��B�й����� | |
| ����2��3.841ʱ����95%�İ����ж�����A��B�й����� | |
| ����2��6.635ʱ����99%�İ����ж�����A��B�й����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{6}$ | B�� | $\frac{��}{12}$ | C�� | $\frac{1}{3}$ | D�� | $\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
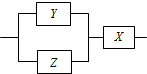 ��ͼ����X��Y��Z��3�ͬ��Ԫ�����ӳ�ϵͳN��ÿ��Ԫ���Ƿ�����������������Ԫ����Ӱ�죬��֪Ԫ��X��Y��Z���������ĸ�������Ϊ0.8��0.7��0.9����ϵͳN���������ĸ�����0.776��
��ͼ����X��Y��Z��3�ͬ��Ԫ�����ӳ�ϵͳN��ÿ��Ԫ���Ƿ�����������������Ԫ����Ӱ�죬��֪Ԫ��X��Y��Z���������ĸ�������Ϊ0.8��0.7��0.9����ϵͳN���������ĸ�����0.776���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �� | 0 | 1 | 2 | 3 | 4 |
| p | $\frac{1}{120}$ | x | y | z | $\frac{1}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -1 | C�� | 4 | D�� | -4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{6}$ | B�� | $\frac{1}{5}$ | C�� | $\frac{4}{5}$ | D�� | $\frac{5}{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | $\frac{1}{3}$ | C�� | -3 | D�� | $-\frac{1}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com