
分析 由题意,知X取0,1,2,求出概率,即可求解EX.
解答 解:由题意,知X取0,1,2,它取每个值的概率都符合等可能事件的概率公式,即 P(X=0)=$\frac{{C}_{7}^{2}}{{C}_{10}^{2}}$=$\frac{7}{15}$,
P(X=1)=$\frac{{C}_{7}^{1}{C}_{3}^{1}}{{C}_{10}^{2}}$=$\frac{7}{15}$,
P(X=2)=$\frac{{C}_{3}^{2}}{{C}_{10}^{2}}$=$\frac{1}{15}$.
于是EX=0×$\frac{7}{15}$+1×$\frac{7}{15}$+2×$\frac{1}{15}$=$\frac{3}{5}$.
故答案为:$\frac{3}{5}$.
点评 本题考查离散型随机变量的数学期望,解题的关键是找到与每个ξ的值相对应的概率P的值.


科目:高中数学 来源: 题型:解答题
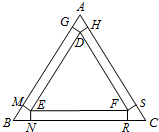 如图:在边长为6米的等边△ABC钢板内,作一个△DEF,使得△DEF的三边到△ABC所对应的三边之间的距离均x(0<x<$\frac{2}{3}$$\sqrt{3}$)米,过点D分别向AB,AC边作垂线,垂足依次为G,H;过点E分别向AB,BC边作垂线,垂足依次为M,N;过点F分别向BC,AC边作垂线,垂足依次为R,S.接着在△ABC的三个内角处,分别沿DG,DH、EM,EN、FR,FS进行切割,割去的三个全等的小四边形分别为AGDH、BMEN、CRFS.然后把矩形GDEM、NEFR、SFDH分别沿DE、EF、FD向上垂直翻折,并对翻折后的钢板进行无缝焊接(注:切割和无缝焊接过程中的损耗和费用忽略不计),从而构成一个无盖的正三棱柱蓄水池.
如图:在边长为6米的等边△ABC钢板内,作一个△DEF,使得△DEF的三边到△ABC所对应的三边之间的距离均x(0<x<$\frac{2}{3}$$\sqrt{3}$)米,过点D分别向AB,AC边作垂线,垂足依次为G,H;过点E分别向AB,BC边作垂线,垂足依次为M,N;过点F分别向BC,AC边作垂线,垂足依次为R,S.接着在△ABC的三个内角处,分别沿DG,DH、EM,EN、FR,FS进行切割,割去的三个全等的小四边形分别为AGDH、BMEN、CRFS.然后把矩形GDEM、NEFR、SFDH分别沿DE、EF、FD向上垂直翻折,并对翻折后的钢板进行无缝焊接(注:切割和无缝焊接过程中的损耗和费用忽略不计),从而构成一个无盖的正三棱柱蓄水池.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 锐角三角形 | C. | 直角三角形 | D. | 钝角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | (?p)∨q | C. | p∧(?q) | D. | (?p)∧(?q) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 8 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{10}}}{10}$ | B. | $\frac{{\sqrt{10}}}{10}$ | C. | $-\frac{{\sqrt{5}}}{5}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com