练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．已知△ABC的三个内角满足sinA：sinB：sinC=5：11：13，则△ABC是（　　）
    A．等腰三角形B．锐角三角形C．直角三角形D．钝角三角形

    分析 由条件利用正弦定理可得a：b：c=5：11：13，C为最大角．再由余弦定理可得cosC=$\frac{{a}^{2}{+b}^{2}{-c}^{2}}{2ab}$＜0，可得C为钝角，从而得出结论．

    解答 解：由△ABC的三个内角满足sinA：sinB：sinC=5：11：13，利用正弦定理可得a：b：c=5：11：13，
    设a=5k，则b=11k，c=13k，故C为最大角．
    由余弦定理可得cosC=$\frac{{a}^{2}{+b}^{2}{-c}^{2}}{2ab}$=$\frac{2{5k}^{2}+12{1k}^{2}-16{9k}^{2}}{11{0k}^{2}}$=-$\frac{23}{110}$＜0，
    可得C为钝角，故△ABC是钝角三角形，
    故选：D．

    点评 本题主要考查正弦定理和余弦定理的应用，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

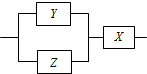    1．如图，用X、Y、Z这3类不同的元件连接成系统N，每个元件是否正常工作不受其它元件的影响，已知元件X、Y、Z正常工作的概率依次为0.8、0.7、0.9，则系统N正常工作的概率是0.776．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知函数$f（x）=\left\{\begin{array}{l}lo{g_2}x+2，x＞0\\{3^x}，x≤0\end{array}\right.$，则$f[f（\frac{1}{8}）]$的值（　　）
    A．3B．$\frac{1}{3}$C．-3D．$-\frac{1}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知数列{an}满足a1=2，an+1=$\frac{{1+{a_n}}}{{1-{a_n}}}$，则a15等于（　　）
    A．2B．-3C．-$\frac{1}{2}$D．$\frac{1}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．已知向量$\vec m$与$\vec n$的夹角是$\frac{π}{3}$，且$（{\vec m-\vec n}）•\vec m=0$，则$\frac{{|{\vec m}|}}{{|{\vec n}|}}$=$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．已知△ABC在正方形网格中的位置如图所示，则cos∠ABC=$\frac{3}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．有10件产品，其中3件是次品，从中任取2件，若X表示取到次品的件数，则EX=$\frac{3}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．设$\frac{1+2i}{2-i}$=a+bi（a，b∈R），其中i是虚数单位，则a+b=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知函数$f（x）=|x|-\frac{2}{x-1}$．
    （1）试讨论函数f（x）在区间（-∞，0）上的单调性；
    （2）若当x∈（b，a）（b＞0）时，函数y=loga（f（x））（a＞0且a≠1）的取值范围恰为（-∞，0），求实数a，b的值．

    查看答案和解析>>

    同步练习册答案