
分析 因为a2是a1和a4的等比中项,所以(a1+d)2=a1(a1+3d),继而求得a1=d,从而$\frac{1}{{b}_{1}}+\frac{1}{{b}_{2}}+…+\frac{1}{{b}_{n}}$的式子即可求得,列式求解即得到d的取值范围.
解答 解:因为a2是a1和a4的等比中项,所以(a1+d)2=a1(a1+3d),
解得a1=d>0,所以an=nd,因此,bn=2nd,
故,$\frac{1}{{b}_{1}}+\frac{1}{{b}_{2}}+…+\frac{1}{{b}_{n}}$=$\frac{1}{d}[\frac{1}{2}+\frac{1}{{2}^{2}}+…+\frac{1}{{2}^{n}}]$=$\frac{1}{d}[1-\frac{1}{{2}^{n}}]<\frac{1}{d}≤2$,
所以,$d≥\frac{1}{2}$,
故答案为:[$\frac{1}{2},+∞$).
点评 本题主要考查等差数列和等比数列的综合应用,属于难度较大的题目,在高考中常在选择填空压轴出现.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
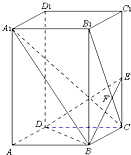 如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.
如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 16+8$\sqrt{3}$ | B. | 16+4$\sqrt{3}$ | C. | 48+8$\sqrt{3}$ | D. | 48+4$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2$\sqrt{2}$,4) | B. | [2$\sqrt{2}$,$\sqrt{2}$+2] | C. | (-∞,2$\sqrt{2}$] | D. | [2$\sqrt{2}$,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com