
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①根据两直线相互垂直时,A1A2+B1B2=0,列出方程,求出m的值即可;
②根据导数的定义,求出$\underset{lim}{k→0}$$\frac{f({x}_{0}-k)-f({x}_{0})}{2k}$的值即可;
③随机变量x~N(0,1),若P(-1<x<0)=$\frac{1}{2}$-P不是命题;
④根据最小二乘法求回归直线方程的方法,判断命题正确;
⑤根据分类变量x与y的随机变量x2的观测值越大,x与y的相关性越强,判断命题正确.
解答 解:对于①,当直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直时,
(m+2)(m-2)+3m•(m+2)=0,解得m=-2或m=$\frac{1}{2}$,∴①错误;
对于②,当f′(x0)=2时,
$\underset{lim}{k→0}$$\frac{f({x}_{0}-k)-f({x}_{0})}{2k}$=$\frac{1}{2}$•$\underset{lim}{k→0}$$\frac{f{(x}_{0}-k)-f{(x}_{0})}{k}$=$\frac{1}{2}$•f′(x0)=$\frac{1}{2}$×2=1,∴②正确;
对于③,随机变量x~N(0,1),若P(-1<x<0)=$\frac{1}{2}$-P,不是命题,∴③错误;
对于④,根据最小二乘法求回归直线方程的方法,知:
最小二乘法求回归直线方程,是求使$\sum_{i=1}^{n}$(yi-bxi-a)2最小的a,b的值,∴④正确;
对于⑤,对于分类变量x与y,它们的随机变量x2的观测值越大,x与y的相关性就越强,
∴⑤正确;
综上,正确的命题是②④⑤.
故选:C.
点评 本题通过命题真假的判断,考查了直线方程的应用问题,导数的定义以及概率与统计的应用问题,是综合性题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2017届江西省红色七校高三上学期联考一数学(理)试卷(解析版) 题型:选择题
下列说法正确的是( )
A. ,“
,“ ”是“
”是“ ”的必要不充分条件
”的必要不充分条件
B.“ 为真命题”是“
为真命题”是“ 为真命题”的必要不充分条件
为真命题”的必要不充分条件
C.命题“ ,使得
,使得 ”的否定是:“
”的否定是:“ ,
, ”
”
D.命题 :“
:“ ,
,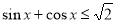 ”,则
”,则 是真命题
是真命题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 36 | B. | 48 | C. | 56 | D. | 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{5}$+2 | B. | 2$\sqrt{5}$ | C. | 4$\sqrt{2}$+2 | D. | 4$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com