
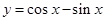 的图象向左平移
的图象向左平移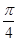 个单位,所得函数图象关于原点对称;
个单位,所得函数图象关于原点对称;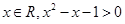 ”,则命题p的否定为:“任意
”,则命题p的否定为:“任意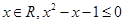 ”;
”;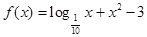 的零点有2个;
的零点有2个;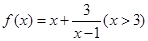 在
在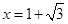 处取最小值;
处取最小值;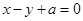 与圆
与圆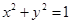 交于不同两点A、B,O为坐标原点,则“
交于不同两点A、B,O为坐标原点,则“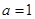 ”是“向量
”是“向量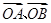 满足
满足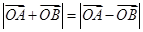 ”的充分不必要条件.
”的充分不必要条件. 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源:不详 题型:填空题
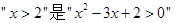 的充分不必要条件;
的充分不必要条件;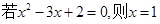 ”的逆否命题为“
”的逆否命题为“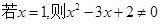 ”;
”;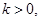 方程
方程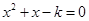 有实根”的否定是:“
有实根”的否定是:“ 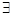
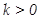 ,方程
,方程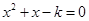 无实根”;
无实根”;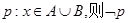 是
是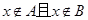 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
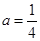 ”是“对任意的正数
”是“对任意的正数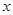 ,均有
,均有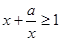 ”的充分非必要条件
”的充分非必要条件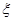 服从正态分布N(2,22),则D(
服从正态分布N(2,22),则D(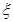 )=2
)=2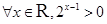 的否定是
的否定是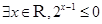
| A.④ | B.①④ | C.①②④ | D.①②③④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ),使sinx+cosx=
),使sinx+cosx=  ;
; - x)既有最大值和最小值,又是偶函数;
- x)既有最大值和最小值,又是偶函数;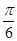 |的最小正周期为p.其中错误的命题为
|的最小正周期为p.其中错误的命题为 查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.“ ”是“ ”是“ ”的充分不必要条件. ”的充分不必要条件. |
B.“ ”是“ ”是“ ”的必要不充分条件. ”的必要不充分条件. |
C.命题“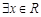 ,使得 ,使得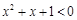 ”的否定是:“ ”的否定是:“ ,均有 ,均有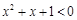 ”. ”. |
D.命题“若 ,则 ,则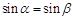 ”的逆否命题为真命题. ”的逆否命题为真命题. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 若
若 则
则 或
或 ;命题
;命题 :平面内与两个定点
:平面内与两个定点 的距离的和等于常数的点的轨迹叫做椭圆,则下列结论错误的是_______▲___________(填序号)
的距离的和等于常数的点的轨迹叫做椭圆,则下列结论错误的是_______▲___________(填序号) ”为假命题; ②“
”为假命题; ②“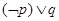 ”为假命题;
”为假命题; ”为真命题; ④“
”为真命题; ④“ ”为真命题.
”为真命题.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 的法向量分别为
的法向量分别为 ,则
,则 ;
; ,则
,则 ;
; ,则
,则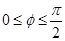 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com