

分析 (Ⅰ)欲证明A1O⊥CE,只需推知A1O⊥平面BCDE即可;
(Ⅱ)根据直线与平面垂直的性质推知OA1,OB,OC两两垂直.所以以O为原点,OB,OC,OA1分别为x,y,z轴建立空间直角坐标系(如图2).结合平面A1CE的一个法向量和直线与平面所成角的正弦求法解答即可;
(Ⅲ)利用假设法进行解答:如图3,假设在侧棱A1C上存在点P,使得BP∥平面A1OF.设$\overrightarrow{{A_1}P}=λ\overrightarrow{{A_1}C}$,λ∈[0,1].由菱形BCDE的性质得到CE⊥BD,结合(Ⅰ)可知:CE⊥平面A1OF.故$\overrightarrow{CE}=(-1,-\sqrt{3},0)$为平面A1OF的一个法向量.据此进行解答.
解答 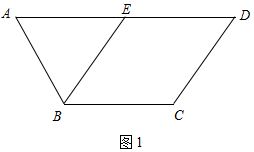 解:(Ⅰ)如图1,在等腰梯形ABCD中,
解:(Ⅰ)如图1,在等腰梯形ABCD中,
∵BC∥AD,$BC=\frac{1}{2}AD=2$,∠A=60°,E为AD中点,
∴△ABE为等边三角形.
如图2,∵O为BE的中点,
∴A1O⊥BE.
又∵平面A1BE⊥平面BCDE,且平面A1BE∩平面BCDE=BE,
所以A1O⊥平面BCDE,所以A1O⊥CE;
(Ⅱ)如图2,连结OC,由已知得CB=CE,又O为BE的中点,
∴OC⊥BE.
由(Ⅰ)知A1O⊥平面BCDE,
∴A1O⊥BE,A1O⊥OC,
∴OA1,OB,OC两两垂直.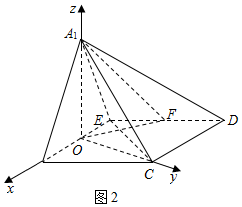
以O为原点,OB,OC,OA1分别为x,y,z轴建立空间直角坐标系(如图2).
∵BC=2,易知$O{A_1}=OC=\sqrt{3}$.
∴${A_1}(0,0,\sqrt{3}),B(1,0,0),C(0,\sqrt{3},0),E(-1,0,0)$,
∴$\overrightarrow{{A_1}B}=(1,0,-\sqrt{3}),\overrightarrow{{A_1}C}=(0,\sqrt{3},-\sqrt{3}),\overrightarrow{{A_1}E}=(-1,0,-\sqrt{3})$.
设平面A1CE的一个法向量为n=(x,y,z),
由$\left\{{\begin{array}{l}{n•\overrightarrow{{A_1}C}=0}\\{n•\overrightarrow{{A_1}E}=0}\end{array}}\right.$得$\left\{\begin{array}{l}\sqrt{3}y-\sqrt{3}z=0\\-x-\sqrt{3}z=0.\end{array}\right.$即$\left\{\begin{array}{l}y-z=0\\ x+\sqrt{3}z=0.\end{array}\right.$
取z=1,得$n=(-\sqrt{3},1,1)$.
设直线A1B与平面A1CE所成角为θ,
则$sinθ=|{cos?\overrightarrow{{A_1}B},n>}|=|{\frac{{-\sqrt{3}-\sqrt{3}}}{{2×\sqrt{5}}}}|=\frac{{\sqrt{3}}}{{\sqrt{5}}}=\frac{{\sqrt{15}}}{5}$.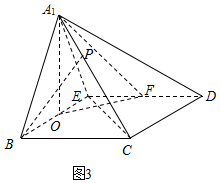
所以直线A1B与平面A1CE所成角的正弦值为$\frac{{\sqrt{15}}}{5}$.
(Ⅲ)如图3,假设在侧棱A1C上存在点P,使得BP∥平面A1OF.
设$\overrightarrow{{A_1}P}=λ\overrightarrow{{A_1}C}$,λ∈[0,1].
∵$\overrightarrow{BP}=\overrightarrow{B{A_1}}+\overrightarrow{{A_1}P}=\overrightarrow{B{A_1}}+λ\overrightarrow{{A_1}C}$,
∴$\overrightarrow{BP}=(-1,0,\sqrt{3})+λ(0,\sqrt{3},-\sqrt{3})=(-1,\sqrt{3}λ,\sqrt{3}-\sqrt{3}λ)$.
易证四边形BCDE为菱形,且CE⊥BD,
又由(Ⅰ)可知,A1O⊥CE,所以CE⊥平面A1OF.
所以$\overrightarrow{CE}=(-1,-\sqrt{3},0)$为平面A1OF的一个法向量.
由$\overrightarrow{BP}•\overrightarrow{CE}=(-1,\sqrt{3}λ,\sqrt{3}-\sqrt{3}λ)•(-1,-\sqrt{3},0)=1-3λ=0$,得$λ=\frac{1}{3}∈[0,1]$.
所以侧棱A1C上存在点P,使得BP∥平面A1OF,且$\frac{{{A_1}P}}{{{A_1}C}}=\frac{1}{3}$.
点评 本题综合考查了直线与平面平行、垂直的判定,直线与平面所成的角以及空间中直线与直线之间的位置关系.难度较大,需要熟练掌握空间直角坐标系的建立与应用.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 2e | D. | 2e2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
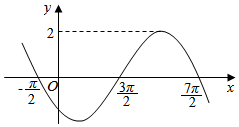
| A. | A=2,ω=2,φ=$\frac{3π}{4}$ | B. | A=2,ω=2,φ=$\frac{5π}{4}$ | C. | A=2,ω=$\frac{1}{2}$,φ=$\frac{3π}{4}$ | D. | A=2,ω=$\frac{1}{2}$,φ=$\frac{5π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | $-\frac{5}{2}$ | C. | -2 | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
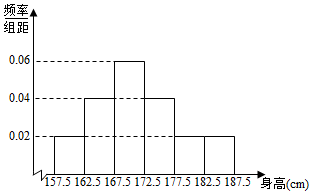 某省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布N(170.5,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第1组[157.5,162.5),第2组[162.5,167.5),…,第6组[182.5,187.5],如图是按上述分组方法得到的频率分布直方图.
某省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布N(170.5,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第1组[157.5,162.5),第2组[162.5,167.5),…,第6组[182.5,187.5],如图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com