
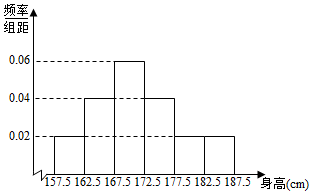
 某省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布N(170.5,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第1组[157.5,162.5),第2组[162.5,167.5),…,第6组[182.5,187.5],如图是按上述分组方法得到的频率分布直方图.
某省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布N(170.5,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第1组[157.5,162.5),第2组[162.5,167.5),…,第6组[182.5,187.5],如图是按上述分组方法得到的频率分布直方图.分析 (I)计算平均身高用组中值×频率,即可得到结论;
(II)先理解频率分布直方图横纵轴表示的意义,横轴表示身高,纵轴表示频数,即每组中包含个体的个数;
根据频数分布直方图,了解数据的分布情况,知道每段所占的比例,从而求出这50名男生身高在177.5cm以上(含177.5cm)的人数;
(III)先根据正态分布的规律求出全市前130名的身高在182.5cm以上的50人中的人数,确定ξ的可能取值,求出其概率,即可得到ξ的分布列与期望.
解答 解:(Ⅰ)根据频率分布直方图,得我校高三年级男生平均身高为$\overline{x}$=160×0.02×5+165×0.04×5+170×0.06×5+175×0.04×5+180×0.02×5+185×0.02×5=171.5,
∴高于全市的平均值170.5;(4分)
(Ⅱ)由频率分布直方图知,后两组频率为0.2,
∴人数为0.2×50=10,
即这50名男生身高在177.5cm以上(含177.5 cm)的人数为10人;…(6分)
(Ⅲ)∵P(170.5-3×4<ξ≤170.5+3×4)=0.9974,
∴P(ξ≥182.5)=$\frac{1-0.9974}{2}$=0.0013,
∴0.0013×100 000=130,
全省前130名的身高在182.5 cm以上,这50人中182.5 cm以上的有5人;
∴随机变量ξ可取0,1,2,于是
P(ξ=0)=$\frac{{C}_{5}^{2}}{{C}_{10}^{2}}$=$\frac{2}{9}$,P(ξ=1)=$\frac{{C}_{5}^{1}{C}_{5}^{1}}{{C}_{10}^{2}}$=$\frac{5}{9}$,P(ξ=2)=$\frac{{C}_{5}^{2}}{{C}_{10}^{2}}$=,
∴Eξ=0×$\frac{2}{9}$+1×$\frac{5}{9}$+2×$\frac{2}{9}$=1.…(12分)
点评 本题考查了频率分布直方图的应用问题,也考查了离散型随机变量的期望与方差的计算问题,属于中档题.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,平面ABCD⊥平面ABEF,四边形ABCD是矩形,四边形ABEF是等腰梯形,其中AB∥EF,AB=2AF,∠BAF=60°,O,P分别为AB,CB的中点,M为△OBF的重心.
如图,平面ABCD⊥平面ABEF,四边形ABCD是矩形,四边形ABEF是等腰梯形,其中AB∥EF,AB=2AF,∠BAF=60°,O,P分别为AB,CB的中点,M为△OBF的重心.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
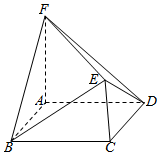 如图所示的多面体EF-ABCD中,AF⊥底面ABCD,AF∥CE,四边形ABCD为正方形,AF=2AB=2CE.
如图所示的多面体EF-ABCD中,AF⊥底面ABCD,AF∥CE,四边形ABCD为正方形,AF=2AB=2CE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com